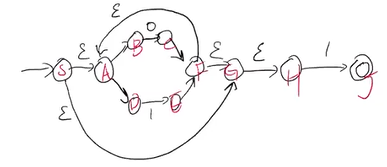
instructor: Yizhou Zhang

E21736 TTh 10-12:00

assn * 6 (63%) + secret test (10%) + fe (25%)

Week 1. Jan 10
Week 2. Jan 17
Week 3. Jan 24
Week 4. Jan 31
Week 5. Feb 7
Week 6. Feb 14
Week 8. Feb 28
Week 9. Mar 7
Week 10. Mar 14
Week 11. Mar 21
Week 12. Mar 28
Week 13. Apr 4

Week 1. Jan 10

big picture:

front end (machine independent)
- lexical analysis (tokenization)
- parsing: create AST
- semantic analysis: eg decorate AST with types
- intermediate code generation
back end
- optimizations; code generation
- register allocation and optimization

bigger picture: compiler => assembler => linker => loader

lexing/tokenization

if (b == c) /* ... */ a += "hi";
^  ^^ ^  ^^ ^         ^ ^  ^   ^

tokens: integer literal, string literals, keywords, operators, comment

given input string, we ignore comments, whitespaces (javadoc comments are exception).

the token class includes token type + attribute + metadata (eg source location)

eg. naive scanning identifier

while true:
    auto c = input.read()
    if !idChar(c):
        break
    id.append(c)

challenges: no backtracking (cannot handle overlapping tokens), no lookaheads

improved:

while idChar(input.peek()):
    id.append(input.read())

one can use regular expressions to define legal tokens to synthesize such lexer code.

R	L(R)	meaning
a	{"a"}
ϵ	{""}
R\|S	L(R) ∪ L(S)	alternation
R⋅S	{rs: r∈L(R), s∈L(S)}	concatenation
R*	L(ϵ) ∪ L(R) ∪ L(RR) ∪ ...	kleene star

extensions

R	L(R)
R?	R\|ϵ
R+	R(R*)
[abc]=[a-c]	a\|b\|c
[^ab]	any char not a or b
.	[^\n]
[^]	any char

lex generators: lex/flex/jflex/...

input: RE + action for each token
output: node that resulted action on matched token
actions:
- create/discard tokens
- raise errors
- side effects
abbreviations
- eg digit = [0-9]
- posint = [1-9]{digit}*
- id = [a-z]{id}*|[a-z] (note: not an RE)

language matching token rule: always match the longest token.

eg. how would java tokenize elsex = 0 ? most languages will treat elesx as an identifier.

eg. how would java tokenize x = +++y ?

if we follow longest token rule, then we have "x" "=" "++" "+" "y", and we have errors.
it would typecheck if we treated it as 3 plus tokens
in Joos, it does not support ++, so output error

eg. how would java tokenize a++b ?

can have "a" "++" "a" and faills parsing
can have "a" "+" "+" "a" and passes parsing
in Joos, we would have "a" "++" "a" and reject

eg. how would java tokenize List<List<Integer>> ?

if we follow longest token rule, then we treat >> as one token and fail
java fixes it by adding a special rule

how does lexer generator work? given spec

spec = re1 {act}
 | re2 {act}
 | ...
// in decreasing order

it does spec => NFA => DFA => loop + table.

defn. a DFA consist of:

initial state $q_0$
alphabet Σ
final state F
transition function $\delta(q,c)=q'$

auto q = q0
while i <= len(input):
    q = delta(q, input[i]):
    ++i
if q in F:
    ...

Week 2. Jan 17

computing delta

strawman idea: directly map RE to DFA. but things like R1="IF",R2="IDENT" do not not work in general. we need to convert to NFA first.

defn. an NFA is a DFA plus

transitions labelled by ϵ
multiple exit arrows with same label
accepts if there is any way to reach final state

algo. (RE to NFA method) suppose $[[R]]$ denotes a DFA for a regular expression with one enter and one exit state. we use base cases:

               a
[[a]] = -> ◯ ---> ◎

               ϵ
[[ϵ]] = -> ◯ ---> ◎

and induction cases

                       ϵ
[[R1⋅R2]] = -> [[R1]] ---> [[R2]]  (change R1's final state to non-final)

 
                  [[R1]]
               ϵ /       \ ϵ
[[R1|R2]] =  -> ◯        ◎       (change R1,R2's final state to non-final)
               ϵ \       / ϵ
                  [[R2]]

                 ϵ          ϵ
           -> ◯ ---> [[R]] ---> ◎
               |       ^ |       ^
[[R*]] =       |       | | ϵ     |  (change R's final state to non-final)
               |       +-+       |
               +-----------------+
                        ϵ

eg. convert (0|1)*1 to NFA.

NFA-DFA idea: a DFA state = set of all NFA states that can be reached by reaching same sequence of symbols.

defn. the ϵ-closure of q is the set of states reachable from q using >= 0 ϵ-edges.

base case: $q\in\epsilon-\mathrm{closure}(q)$ ;
inductive: $q'\rightarrow q''\text{ via }\epsilon,q'\in\epsilon-\mathrm{closure}(q)\implies q''\in\epsilon-\mathrm{closure}(q)$

eg. ϵ-closure(G) = {G, H}, ϵ-closure(F) = {F, G, H, A, B, D}, ϵ-closure({G, F}) = ϵ-closure(G) ∪ ϵ-closure(F).

algo. (computing ϵ-closure)
equations:

ϵ-closure[q][q] = true
ϵ-closure[q][q'] = $\bigvee_{q''\rightarrow q'\text{ via }\epsilon}$ ϵ-closure[q][q'']

compute(q):
    for all states q' in NFA:
        ϵ-closure[q][q'] = false
    worklist = {q}
    // invariant: q' equation is not satisfied => q ∈ worklist'
    while worklist:
        auto q' = worklist.pop()
        update ϵ-closure[q][q'] per its equation
        if ϵ-closure[q][q'] changed:
            for every q' such that q'' -> q' via ϵ:
                add q'' to worklist

correctness:

by invariant: equation of each state is satisfied on termination
why it terminates: ϵ-closure[q][q'] can only change from 0 to 1, and there are finite number of them

complexity: O(N), where N is number of NFA states.

algo. (construct DFA from NFA)

initial state of DFA is $\epsilon-\textrm{closure}(q_0)$ where $q_0$ is NFA's start state
states of DFA: all subsets of DFA states
transitions of DFA: $\delta(Q,x)=\epsilon-\textrm{closure}(\bigcup_{q\in Q}\{q':q\rightarrow q'\text{ via }x\})$
final states: Q is final state of DFA if any $q\in Q$ is final state in NFA

eg. convert (0|1)*1 to DFA.

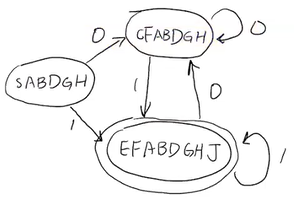
this DFA is not minimal, we can minimize it. we want to ask when two DFA states are equivalent.

defn. two DFA states $Q_1,Q_2$ are not equivalent when

one of them is final state, and the other is not;
there exists $x$ such that $\delta(Q_1,x)$ and $\delta(Q_2,x)$ are not equivalent.

use worklist algo, we start with every pair of states being equivalent, and unequate them.

theorem. (myhill-nerode) for any DFA, there exists a unique minimal DFA accepting some input.

the states SABDGH and CFABDGH are equivalent, so they can be merged.

eg. suppose we have a spec

spec = R1   {act 1}
       | R2 {act 2}

and we generate an NFA and a DFA

    ◯ ... ◎ A
  /
◯                    -----> ◯ -> ... ◎ AB
  \
    ◯ ... ◎ B

the final state contains both A and B. what action should lexer do? it should do action A because of decreasing priority.

finally, the generated code should do

run the DFA until stuck
backtrack to the last final state reached (longest matching token rule)

eg. suppose R1=abc, R2=(abc)*d. what does abcabc...abcx match?
lexer will reach x and fail, then it backs up to beginning and match R1. then it starts from the second abc and reach x again, ... the time complexity is O(N^2).

minimization algo of DFA exists to reduce complexity to O(N).

interpreting REs by derivatives

start from regular expression RE0, receive input $x_1$ , then we transit to regular expression RE1 and so on..

$RE_{i+1}$ is derivative of $RE_i$ upon consuming $x_{i+1}$ .

defn. the derivative of regular expression $R$ wrt $a$ , $\partial aR$ is

base cases:
- $\partial aa=\epsilon$
- $\partial ab=\varnothing$ (re that accepts nothing)
- $\partial a\epsilon=\varnothing$
inductive:
- $\partial a(R_1+R_2)=\partial aR_1+\partial aR_2$
- $\partial aR^*=(\partial aR)R^*$
- $\partial a(R_1R_2)=(\partial aR_1)R_2+v(R_1)(\partial aR_2)$ $\partial a (R_{1} R_{2}) = (\partial a R_{1}) R_{2} + v (R_{1}) (\partial a R_{2})$
  - where $v(R_1)=\epsilon$ if $R_1$ accepts empty string, otherwise $\varnothing$

parsing

we use context-free-grammar (rewrite does not depend on context)

eg.

start symbol: S
terminals: + * n ( )
nonterminals: S, E
productions:
  S -> S + S | S * S | E
  E -> n | ( S )

defn. a derivation is sequence of rewrites from start symbol to a token stream.

at each step, $\alpha X\beta\rightarrow\alpha\gamma\beta$ , where $X\rightarrow\gamma$ is a production.

notation.

we use $L(G)$ to denote the language of grammar G;
a token stream $\in L(G)$ iff there is a derivation using G;
uppercase english letters are nonterminals;
lowercase english letters are terminals;
greek letters are strings of symbols.

eg. how to derive (1+4)+2 ?

S
S + S
E + S             // leftmost derivation:
( S ) + S         // expand leftmost terminal first
( S + S ) + S
( E + E ) + E
( 1 + 4 ) + 2

S
S + S
S + E
S + 2             // rightmost derivation
...

its parse tree is

leftmost derivation corresponds to top-down parsing; rightmost derivation corresponds to bottom-up parsing.

defn. G is ambiguous if some string in L(G) has multiple parse trees.

eg. 1+2*3 has two parse trees, so the grammar above is ambiguous. the precedence of + and * is not enforced.

eg. 1+2+3 has two parse trees. the associativity of + is not enforced.

fixing ambiguity:

S -> S + T | T
T -> T * F | F
F -> n | ( S )

// precedence left +
// precedence left *

this defines the same language but unambiguous because

cannot have + under *
cannot have + under RHS of +

many parser generators allow specifying precedence and associativity.

eg. dangling else problem

S -> if E then S
   | if E then S else S
   | ...

how do we parse if E1 then if E2 then S1 else S2 ? we can let the else belong to the inner if, or let it belong to the outer if. most languages choose the first parse (the "closest-if rule").

if E1 then
    if E2 then S1
    else S2

this grammar is ambiguous. to fix it, we observe there are two kinds of statements

U: if-statements ending in an unmatched then => should not be followed by else
M: all other statements

we can fix using

S -> M | U
M -> if E then M else M
   | ...
U -> if E then S
   | if E then M else U

// precedence noassoc if
// precedence noassoc else

eg. needing context: how to parse HashTable<K, V> x; ? there are 2 solutions

lexer receives feedback from later stages from compiler (not ideal)
parser creates parse tree with ambiguous nodes; ambiguity is resolved at later stage

eg. significant whitespace (python): lexer inserts extra indent/dedent tokens.

Week 3. Jan 24

LL parsing

aka top-down parsing / recursive-descent parsing

eg. given S-expression (scheme)

S -> ( L ) | x
L -> ϵ | S L

we parse like this

class SExpr {}
class ListExpr extends SExpr {}
class Id extends SExpr {}

SExpr parseS() {
    switch (peek()) {
        case LPAREN:    // S -> (L)
            consume();  // LPAREN
            List<SExpr> l = parseL();
            consume();  // RPAREN
            return new ListExpr(l);
        case IDENT:     // S -> x
            String id = consume();  // IDENT
            return new Id(id);
        default:
            throw SyntaxError;
    }
}

List<SExpr> parseL() {
    switch (peek()) {
        case ID: case LPAREN:  // S -> S L
            SExpr S = parseS();
            List<SExpr> l = parseL();
            return new List<>(s, new ListExpr(l));
        case LPAREN:  // L ->
            return new List<>();
        default:
            throw SyntaxError;
    }
}

if we parse "(x x)" we get

       ListExpr
          |
      List<SExpr>
      /        \
     /          \
Id("x")        Id("x")

predictive parsing table (PPT) for one lookahead:

	(	x	)
S	S → (L)	S → x	None
L	L → SL	L → SL	L → ϵ

defn. a grammar is LL(1) if a 1-lookahead PPT can be constructed.

LL(k>=2) grammars are not generally used. if $\Sigma$ represents vocabulary, then there are $2^{|\Sigma|}$ columns in a PPT.

to build prediction table, we build 3 tables

Nullable(X): true iff X can derive ϵ
First(X): set of tokens that can start X
Follow(X): set of tokens that can follow X

eg. for the S-expr grammar, we get

Nullable(S) = 0
Nullable(L) = 1

First(L) = (, x
Follow(L) = )

we will build a table such that Cell(x, a) in PPT contains

X → γ where a ∈ First(γ).
X → γ where Nullable(γ) = 1 and a ∈ Follow(X)

claim. (proving string is nullable)

ϵ is nullable;
if X → γ ∈ G and γ is nullable, then X is nullable;
if X is nullable and β is nullable, then Xβ is nullable.

algo. (computing nullable using iterative solving)
equations:

Nullable[x] = $\bigvee_{X\rightarrow\gamma\in G}$ Nullable[γ]
Nullable[γ] =
- 1 if γ = ϵ
- 0 if γ = β
- Nullable[x] ∧ Nullable[β] if γ = Xβ

for each nonterminal X:
    nullable[X] = 0
repeat until no more changes:
    for each X in G:
        update nullable[X] per X equation
return nullable

correctness:

nullable mapping can only flip from false to true
partial correctness: by construction
termination: O(N^2)
- the inner loop has at most O(N) iterations
- the outer loop has at most O(N) iterations since each nonterminal flips at most once

algo. (computing nullable using worklist)

for each nonterminal X:
    nullable[X] = 0
auto worklist = {X: X → ϵ ∈ G}
// invariant: if X's equation is not satisfied, then X is in work list
while worklist is not empty:
    auto X = worklist.pop()
    update nullable[X] per X equation
    if nullable[X] changed:
        for each Z → αXβ ∈ G:
            worklist.add(Z)
return nullable

claim. (proving string is in first set)

a ∈ First(aβ) for all β
if X → γ ∈ G and a ∈ First(γ), then a ∈ First(X)
if a ∈ First(X), then a ∈ First(Xβ)
if Nullable(X) and a ∈ First(β), then a ∈ First(Xβ)

equations:

First(X) = $\bigcup_{X\rightarrow\gamma\in G}$ First(γ)
First(γ) =
- ∅ if γ = ϵ
- {a} if γ = aβ
- First(X) if γ = Xβ and X is not nullable
- First(X) ∪ First(β) if γ = Xβ and X is nullable

we can similarly provide two algos to compute first.

claim. (proving string is in follow set)

if Y → aXβ ∈ G and a ∈ First(β), then a ∈ Follow(X)
if Y → aXβ ∈ G and Nullable(β) = 1 and a ∈ Follow(Y), then a ∈ Follow(X)

equation: Follow(X) = $\bigcup_{Y\rightarrow\alpha X\beta\in G}$ (First(β) ∪ (if Nullable(β) then Follow(Y) else ∅))

eg. failing cases: Cell(X,a) has >= productions.
we can use LL(2+), but it causes state explosion. we can use following tricks:

(1) shared first set:

L -> S | S L  // not LL(1)

fix:
L  -> S L'
L' -> ϵ | L

(2) left recursion

L -> S | L + S  // not LL(k) since First(L+S) = First(S)

fix:
L -> S(+S)*      // parse (+S)* using a loop

Expr parseL() {
    Expr result = parseS();
    while (peek()) {
        consume();  // '+'
        result = new Plus(result, parseS());
    }
    return result;
}

earley parser

problem with top-down parsing: must predict production before seeing entire input going into the production. this is not required for button-up parsing.

earley parser: chooses productions as late as it can

can handle all CFG
can handle ambiguous grammars => creates 'parse forest'

straw man: fork off a parser thread for each possible production.

key idea: simulates threads in poly time by tracking all parses as sets of (earley) items.

an earley item is [A → β•γ, i]
- where A → βγ is a CFG production
- • is current input position
- i is input position where thread for this item was spawned
processes input left-to-right, one token at a time
for each input position $j$ , construct a set of items $I_j$
start from $I_0=$ {[S' → •S, 0]}
CFG accepts input $a_0...a_n$ if $I_n$ contains [S' → S•, 0]

algo. (how to construct $I_j$ ):

for each j:
    do until no changes to I[j]:
        scan:
        if [A→β•cγ,k] ∈ I[j], next token is c:
            add [A→βc•γ,k] to I[j+1]
        predict:
        if [A→β•Cγ,k] ∈ I[j]:
            for all C→γ ∈ G, add [C→•γ,j] to I[j]:
        complete:
        if [C→γ•,k] ∈ I[j] and [A→β•Cδ,m] ∈ I[k]:
            add [A→βC•δ,m] to I[j]

eg.

S -> S + E | E
E -> n | ( S )

input: (1)+2

I[0] = [S'→•S,0], [S→•S+E,0], [S→•E,0], [E→•n,0], [E→•(S),0]

get (:
  I[1] = [E→(•S),0] [S→•S+E,1], [S→•E,1], [E→•n,1], [E→•(S),1]
get 1:
  I[2] = [E→n•,1], [S→E•,1], [E→(S•),0], [S→S•+E,1]
get ):
  I[3] = [E→(S)•,0], [S→E•,0], [S'→S•,0], [S→S•+E,0]
get +:
  I[4] = [S→S+•E,0], [E→•n,4], [E→•(S),4]
get 2:
  I[5] = [E→n•,4], [S→S+E•,0], [S'→S•,0], [S→S•+E,0]
                                   ^
                            successful thread

the derivation in successful thread is

S' -> S -> S+E -> S+2 -> E+2 -> (S)+2 -> (E)+2 -> (1)+2

time complexity: O(n^3) for arbitrary CFG; O(n^2) for unambiguous grammars; O(n) for LR(k) grammar with optimization (eg doing lookahead in complete operation)

LR parsing

a specialization of earley parser. we precompute a parsing table (DFA) with which parser knows whether to scan or complete.

aka shift-reduce parser => shift is scan + prediction (closure), reduce is complete

eg. parse the same (1)+2.

	stack	unconsumed
		(1)+2
shift	(	1)+2
shift	(1	)+2
reduce E→n	(E	)+2
reduce S→E	(S	)+2
shift	(S)	+2
reduce E→(S)	E	+2
reduce S→E	S	+2
shift	S+	2
shift	S+2
reduce E→n	S+E
reduce S→S+E	S

LR parsing table: given current stack and current lookahead token, tells whether shift or reduce (and which production)

the table can be ambiguous: shift-reduce conflicts and reduce-reduce conflicts.

Week 4. Jan 31

in LR(k) parser, it has

k lookahead tokens
a stack of symbols and automaton states (parser state)

LR(0) parser

the automaton state is a set of LR(0) items [X → α•β] (not parser state).

algo. (construct LR(0) automaton)

initial_state = ϵ-closure[S' → •S$]
do until no more states or transitions:
1. for each symbol to right of • in some state:
  1. add transition to a state with all matching terms advanced and closure taken

eg.

S -> S + E | E
E -> n | ( S )

how to use the DFA:

when we read a token and transit, push token and state to stack
if we read a token that does not have transition, then it is syntax error.
after reaching a terminal state X→γ•, we reduce. we pop γ and its states from stack and push X into stack. find next state by walking back |γ| states.

eg. parse (1+2).

	stack	unconsumed input
	o	(1+2)$
shift 2	o(₂	1+2)$
shift 1	o(₂1₁	+2)$
reduce E→n	o(₂E	+2)$
goto 3	o(₂E₃	+2)$
reduce S→E	o(₂S	+2)$
goto 4	o(₂S₄	+2)$
shift 5	o(₂S₄+₅	2)$
shift 1	o(₂S₄+₅2₁	)$
reduce E→n	o(₂S₄+₅E₇	)$
reduce S→S+E	o(₂S₄	)$
shift 6	o(₂S₄)	$
reduce E→(S)	oE₃	$
reduce S→E	oS₈	$
shift 9	oS₈$₉
reduce S'→S$	S'

SLR parsing: reduce X→γ only if lookahead a ∈ Follow(X).

eg. SLR can help shift-reduce conflict

S -> E + S | E
E -> n | ( S )

LR(1) parsing

an LR(1) item is [X → α•β, λ] = LR(0) item + 1 lookahead set.

note λ are tokens that could appear after β

construction of LR(1) automaton is same as LR(0), however the closure of LR(1) item is different: if state includes [X → α•Yβ, λ], then new state should include items [Y → •γ, λ'] where

Y → γ ∈ CFG
λ' = First(β) if Nullable[β] = false
λ' = First(β) ∪ λ otherwise

eg.

S -> E + S | E
E -> n | ( S )

for unambiguous grammar,

lookahead sets of reduce items do not overlap
lookahead set of a reduce item does not overlap with shift item

eg. precedence left plus

E -> E + E | E * E

+---------------
|E → E+E•    +     <- reduce E→E+E on +
|E → E•+E    ...   <- shift on +
+---------------

+---------------
|E → E*E•    +     <- reduce E→E*E on +
|E → E•+E    ...   <- shift on +
+---------------

the conflict can be solved by specifying

precedence left PLUS;
precedence left TIMES;

LALR(1) parsing

LR(1) automaton has too many states. LALR(1) merges LR(1) states with same LR(0) items into an LALR(1) state.

eg.

two LR(1) states, unambiguous
+------------+     +------------+
|E → n•    + |     |E → n•    $ |
|E → E+n•  + |     |E → E+n•  $ |
+------------+     |------------+

one LALR(1) state, ambiguous
+-------------+
|E → n•    $+ |
|E → E+n•  $+ |
+-------------+

venn diagram:

AST

the parser creates a parse tree, which is different from the AST.

ast design principle: don't fight your language

oop: use class hierarchy with method dispatch: Node class, Unary|binaryExpr class, Stmt class, etc.
fp: use variant type with pattern matching

how do parsers construct ASTs:

recursive descent: recursive function returns AST
bottom-up parser: AST constructed on reduce

eg. specify action on the parser generator

expr := expr:e1 PLUS expr:e2 { RESULT = new BinaryExpr(op.Plus, e1, e2) }

stack before reduce:
( E + E
  ^   ^
  e1  e2

stack after reduce:
( E
  ^
 BinaryExpr(...)

semantic analysis

this pass either

catch semantic errors (no more errors from now on)
returns valid, decorated AST

valid = well-formed

acyclic class hierarchy
no uninitialized variables
no type errors

decorated = extra info useful for later passes

types
data layout

eg. need to resolve names.

package p;
class A {
      ^ // declaration of name
    static int x;
    A A(A A) {
    ^ - ^ = // reference, declaration, reference, declaration
        return (A)A.A(A);
                ^ = - =  // all references
    }
}

how to represent declaration of names?

option 1: declaration as ASTs; references point to declaration's AST
- problems:
  - ASTs not always available: source references bytecodes
  - inefficient: implies we have to do AST traversals in type checking
  - error-prone
options 2: declaration as class objects, method objects, local var objects, etc.

eg.

package p;
import q.*;
class C {
    D y;
    int z = A.x;
    ... y.w.z ...
}

package q;
class D extends C { C w;}

package q;
class C { String z; }

first step: define environment (context/symbol table), which maps symbols to objects:

second step: resolve uses of type names to class objects.

do we want to combine 1st and 2nd steps into a single AST traversal? no, there are mutual recursive classes.

note qualified names like a.b.c.d are deferred until type checking.

third step: preliminary checking on class hierarchy.

notation.

suppose we have code class A extends B implements C, D, E {}, we say super(A) = {B,C,D,E}.
suppose we have code interface F extends G, H, I, we say super(F) = {G,H,I}

defn. $A$ is subtype of $B$ , ie $A<:B$ ,

if $B\in\mathrm{super}(A)$ ;
or if $A<:T$ and $T<:B$ .

defn. Declare(T) = methods and fields that are derived in class/interface T

method m ∈ Declare(T): name(m), sig(m), mods(m), type(m)
- sig includes name and params
field f ∈ Declare(T): name(f), type(f), mods(f)

defn.

Inherit(T) = set of methods and fields inherited into T
Contain(T) = Declare(T) ∪ Inherit(T)
Replace = binary relation between methods
- (m, m') ∈ Replace means 'm replaces m''
- m is static: m hides m'
- m is nonstatic: m overrides m'

Week 5. Feb 7

replace:

if S ∈ Super(T), sig(m) = sig(m'), m' ∈ Contain(S), m ∈ Declare(T), then (m, m') ∈ Replace
- T inherits from S. T and S both define m.
if S ∈ Super(T), m ∈ Contain(S), S' ∈ Super(T), m'∈ Contain(S'), sig(m) = sig(m'), abstract ∈ mods(m'), abstract !∈ mods(m), NoDecl(T, m), then (m, m') ∈ Replace
- T inherits from S and S'. S::m is concrete and S'::m is abstract. T does not define m.
- where NoDecl(T, m) := ∀m' ∈ Declare(T), sig(m') !m sig(m)

inherit:

if m ∈ Contain(S), S ∈ Super(T), NoDecl(T, m), abstract !∈ mods(m), then m ∈ Inherit(T)
- T inherits from S. S defines m.
if m ∈ Contain(S), S ∈ Super(T), NoDecl(T, m); ∀S' ∈ Super(T) ∀m' ∈ Contain(S'), sig(m) = sig(m') => abstract ∈ mods(m'), then m ∈ Inherit(T)
- T inherits from S and S'. S defines m, S' deines m'.
if f ∈ Contain(S), S ∈ Super(T); ∀f' ∈ Declare(T), name(f') != name(f), then f ∈ Inherit(T)

technicality: java.lang.Object is a supertype of all class and interface types. methods equals(Object), hashCode(), toString() are implicitly in the Declare of an interface.

eg. a protected method must not replace a public method.
this translates to ∀(m, m') ∈ Replace, public ∈ mods(m') => protected !∈ mods(m).

eg. a method must not replace a method with a different return type.
this translates to ∀(m, m') ∈ Replace, type(m) = type(m') (no covariance).

symbol table

an ast traversal will decorate the AST with types:

abstract class Expr {
    Optional<Type> type;  // initially null, filled by typechecking
    abstract void typeCheck() throws SemanticError;
}

class BinExpr extends Expr {
    Op op;
    Exp left, right;
    void typeCheck() {
        left.typeCheck();
        right.typeCheck();
        switch (op) {
            case PLUS: {
                if (left.type.eq(Int) && right.type.eq(Int)) {
                    this.type = Int;
                    return;
                } else if (left.type.eq(StringTy) || right.type.eq(StringTy)) {
                    this.type = StringTy;
                    return;
                } else {
                    throw new SemanticError();
                }
            }
            case ...
        }
    }
}

we need context to remember names

class Context {
    Type get(String name) throws UnboundIdent;
    void put(String name, Type type) throws BoundIdent;
}

class LocalVar extends Expr {
    String name;
    void typeCheck(Context c) {
        this.type = c.get(this.name);
    }
}

class LocalVarDeclare extends Stmt {
    String name;
    TypeNode tn;
    void typeCheck(Context c) {
        tn.typeCheck(c);
        try {
            c.get(name);
            throw new SemanticError("already declared");
        } catch (UnboundIdent) {
            c.put(name, tn.type);
        }
    }
}

class Block extends Stmt {
    List<Stmt> stmts;
    void typeCheck(Context c) {
        c.pushFrame();  // or clone and discard
        for (s : stmts) {
            s.typeCheck();
        }
        c.popFrame();
    }
}

implement the context using a stack of hashtables.

entry: push table O(1)
exit: pop table O(1)
put: O(1)
get: O(depth)

AST traversal

ast traversal is used in

environment building
type linking
type check
build CFG
generate intermediate code
generate x86 (with intermediate code)

OO style: all AST nodes have a typeCheck() method that does traversal:

+ all code about AST type in one place
- boilerplate code repeated in all passes
- awkward to add new passes

FP style: a typeCheck() function does pattern matching

+ all code about a pass in one place
- boilerplate
- awkward to add new AST constructors

resolve tension

better programming language features (C# extension methods, OCaml polymorphic variants, Julia multimethods, family polymorphism)
design pattern: data types a la carte (FP), visitor pattern (OOP)

class Visitor {
    void visitBinExpr(BinRxpr e) {}
    void visitIf(If n) {}
    ...
}

class TypeChecker extends Visitor {
    Context c;
    void visitBinExpr(BinExpr r) {
        var t1 = e.left.type, t2 = e.right.type;
        // compare if t1 and t2 are compatible
    }
}

class BinExpr {
    void accept(Visitor v) {
        left.accept(v);
        right.accept(v);
        v.visitBinExpr(this);
    }
}

+ easy to add new passes
+ avoid boilerplate
- awkward to add new AST types

types

at compile time = statically; at run time = dynamically.

static type = type at compile time + type checking at compile time

+ types are approximations of runtime behavior => generate faster code
+ programmer guidance
- annotation is harder (can be somewhat alleviated by type interference)

dynamic typing = values carry types at run time + type checking at run time

- runtime cost
- hard to generate faster code
+ no annotation burden

strong typing ≈ no undefined behaviors

ok to nondeterminism
eg C is not strongly typed

	strong typing	weak typing
static typing	ocaml, haskell	C/C++
static & dynamic typing	Java, C#
dynamic typing	javascript, python	perl, postscript
untyped	λ-calculus, assembly

static type checking:

whether program goes wrong at run time is undecidable
idea: use static type checking to ensure well-typed programs do not go wrong at run time
- program is well-typed if it satisfies the type system (rules)
- sound typing/type safety: statically well-typed => dynamically cannot go wrong
- complete typing: dynamically cannot go wrong => statically well-typed

eg.

Map m = new HashMap();
m.put("foo", "bar");
String s = m.get("foo");  // m.get() returns Object

the program will run successfully. but it does not typecheck in Joos.

the design of a type system is balancing act.

decidability of type checking:

most type systems are decidable (eg Joos)
java's type system is undecidable (because of wildcards supertype constraints)

types in Joos:

τ,σ ::= C (class/interface type)
    | boolean | short | byte | char | int
    |'null type'
    | void (return type)
    | τ[] (τ is C, boolean, ..., int)

types in other languages:

function types τ1 -> τ2
array types τ[] and τ[e] (dependent typing)
product/tuple types τ1 * τ2 * ... * τn
record types {f1: τ1, ..., fn: τn}
- C structs: nominal record types
sum/union/variant types τ1 + ... + τn
algebraic data types data T = x1: τ1 -> T | ... | xn: τn -> T
pointer types
parameterized types class Cell<T> { T content; }
- is a function (type constructor)

formalizing type system:

typing rules: declarative spec for type system
typing judgement form:
- expression: Γ ⊢ e : τ , where Γ iis context, e is expr, τ is static type
- statement: Γ; σ ⊢ S, where σ is return type of current function
type system is a proof system of typing rules

eg. some typing rules

plus: (Γ ⊢ e1: int, Γ ⊢ e2: int) => Γ ⊢ e1 + e2: int
var: x: τ in Γ => Γ ⊢ x: τ
intliteral: Γ ⊢ n: int

eg. typing derivation is a proof tree

\cfrac{\cfrac{}{\Gamma\vdash2:\texttt{int}}\text{(intlit)},\cfrac{\cfrac{y:\texttt{int}\in\Gamma}{\Gamma\vdash y:\texttt{int}}\text{(var)},\cfrac{}{\Gamma\vdash3:\texttt{int}}\text{(intlit)}}{\Gamma\vdash y*3:\texttt{int}}\text{(times)}}{\Gamma\vdash2+y*3:\texttt{int}}\text{(plus)}

where $\Gamma=x:\texttt{bool},y:\texttt{int}$ .

some Joos typing rules:

literals:
- Γ ⊢ 3: int
- Γ ⊢ true: boolean
- Γ ⊢ null: NullType
- Γ ⊢ "123": String
variables:
- x: τ in Γ => Γ ⊢ x: τ
- note a special "this" variable
operators:
- Γ ⊢ e: boolean => Γ ⊢ !e: boolean
- (Γ ⊢ e1: String, Γ ⊢ e2: τ2, τ2 != void) => Γ ⊢ e1 + e2: String
field access:
- (Γ ⊢ e: C, (τ, f) ∈ Contain(C)) => Γ ⊢ e.f: τ
- (static τ f) ∈ Contain(C) => Γ ⊢ C.f: τ
assignment:
- (x: τ1 in Γ, Γ ⊢ e: τ2, τ1 := τ2) => Γ ⊢ x = e: τ1
  - "τ2 is assignable to τ1"

Week 6. Feb 14

assignability (jls sec5):

τ := τ
widening conversions:
- int := char
- short := byte
- int := byte
- int := short
- char is unsigned: 0 ~ 2^16-1
- short is signed: -2^15 ~ 2^15-1
if D <= C then C := D
- if D < C, then D <= C
- C <= C
- if C1 <= C2, C2 <= C3, then C1 <= C3
C := NullType
τ[] := NullType
Object := τ[]
Clonable := τ[]
Serializable := τ[]
if D <= C, then C[] := D[]

eg.

B[] bs = new B[1];
Object[] os = bs;  // typechecks
os[0] = "123";     // typechecks
B b = bs[0];       // runtime problem

java: adds runtime check at every array write: throws ArrayStoreException on 3rd line.

rules (continued):

assignment:
- Γ ⊢ e1: C, Γ ⊢ e2: τ2, "τ1 f" in Contain(C) => Γ ⊢ e1.f = e2
  - field access
- "static τ1 f" in Contain(C), Γ ⊢ e: τ2, τ1 := τ2 => Γ ⊢ C.f = e
  - static field
array:
- Γ ⊢ e1: τ1[], Γ ⊢ e2: τ2, num(τ2) => Γ ⊢ e1[e2]: τ1
- Γ ⊢ e1: τ1[], Γ ⊢ e2: τ2, num(τ2), Γ ⊢ e3: τ3, τ1 := τ3 => Γ ⊢ e1[e2] = e3
- Γ ⊢ e: τ', num(τ') => Γ ⊢ new τ[e]: τ[]
- Γ ⊢ e: τ[] => Γ ⊢ e.length: int
method calls:
- Γ ⊢ e: C, Γ ⊢ e2: τ2, "τ m(τ1,...,τn)" in Contain(C) => Γ ⊢ e.m(e1,...,en): τ
  - instance method
- ... => Γ ⊢ C.m(e1,...,en): τ
  - static method
casts:
- Γ ⊢ e: τ', num(τ), num(τ') => Γ ⊢ (τ) e: τ
- Γ ⊢ e: τ1, τ2 := τ1 => Γ ⊢ (τ2) e: τ2
  - upcast: no runtime check
- Γ ⊢ e: τ1, τ1 := τ2 => Γ ⊢ (τ2) e: τ2
  - downcast: need runtime check
- Γ ⊢ e: τ1, t1 is interface, τ2 is interface/nonfinal class => Γ ⊢ (τ2) e: τ2
  - C implements J, I; wants to cast from I to J
- Γ ⊢ e: τ1, τ2 is interface, τ1 is interface or nonfinal class => Γ ⊢ (τ2) e: τ2
instanceof:
- Γ ⊢ e: τ1, τ2 is reference type, Γ ⊢ (τ2)e: τ2 => Γ ⊢ e instance of τ2: boolean

statement rules: Γ; σ ⊢ S

Γ; void ⊢ return;
Γ ⊢ e: τ, σ := τ => Γ; σ ⊢ return e;
Γ ⊢ e: τ', τ := τ', Γ[x->τ]; σ ⊢ S => Γ; σ ⊢ τ x = e; S
- []: declare new local variable x with type τ
Γ; σ ⊢ S => Γ; σ ⊢ {S};
Γ ⊢ e: boolean, Γ; σ ⊢ S1, Γ; σ ⊢ S2 => Γ; σ ⊢ if (e) S1 else S2;
Γ ⊢ x = e: τ, Γ; σ ⊢ x = e;

dataflow analysis

essense of type system: approximate facts/properties of runtime behavior statistically.

eg. definitive assignment:

public static int f(List<Integer> l) {
    int x;
    try {
        x = l.get(0);
    } catch (IndexoutofBoundsException e) {
        System.err.println("empty list");
    }
    return x;
}

this program does not typecheck in java, since x may not be initialized. this is observed at compile-time.

dataflow analysis is special case of program analysis, which includes:

definite assignment (a4)
reachable statement analysis (a4)
live variable analysis (a4)
null pointer analysis
escape analysis (check if variable is only used inside a method)
exception analysis
termination analysis
in general these are undecidable

live variable analysis

register allocation: assigning registers to program variables
variable x is live at some point = value x may be needed later

eg.

            // live = {a,e}
b = a + 2;
            // live = {b,e}
c = b + b;
            // live = {c,e}
d = c * e;
            // live = {d}
return d;
            // live = {}

<= 2 vars are live at any point => use 2 registers
a, b, c, d are never live together => eax; e => ecx

eg.

int x = y;
f();       // is x is live iff f() terminates? undecidable
return x;

conservative approximation: overestimate liveness.

we compute facts over a control-flow-graph (CFG):

eg. consider

    cmp t1 t2       //I1
    jz l1           //I2
    mov t3, 42      //I3
L1: add t3, t4      //I4

the CFG would be:

I1 -> I2
I2 -> I3 (false)
I3 -> I4
I2 -> I4 (true)

eg. consider code

while (c) {
    x = y + 1;
    if (d) {
        x = y + z;
    }
    z = 1;
}

the CFG would be

simple liveness analysis

an IR-like language:

CFG node	IR-equivalent	use	def
x <- e	move(x, e)	vars(e)	{x}	write
[e1] <- e2	move(mem(e1), e2)	vars(e1) ∪ vars(e2)	∅	mem address write
if e	cjump(e, l1, l2)	vars(e)	∅
start	label(f)	∅	∅
return e	return(e)	vars(e)	∅

expression e := e1 OP e2 | [e] | ....

we use use[n] to denote set of variables read at n, def[n] to denote set of variables written at n.

eg.

use[a <- b+c] = {b, c}
def[a <- b+c] = {a}
use[[a] <- b] = {a, b}
def[[a] <- b] = {}

defn. variable x is live on CFG edge E if there is a path from E to a use of variable, and there is no def of x in between.

we also define

in[n] to be facts true on all incoming edges, or vars that may be live before n executes
- in[n] = use[n] $\cup$ (out[n] - def[n])
out[n] to be facts true on all outgoing edges, or vars that may be live after n executes
- out[n] = $\bigcup_{n'>n}$ in[n']
- n' > n, or n < n' means n' is a successor of n

algo. (using iterative solving to compute in[n])

initialize in[n] := ∅ for all n in CFG
repeat until no more changes to in[n]:
1. for all node n in CFG:
  1. in[n] = use[n] $\cup$ ( $\bigcup_{n'>n}$ in[n'] - def[n])

correctness:

equations must be satisfied on termination => partial correctness
- in[n] can only grow
- in[n] can only grow |V| times, where |V| is # of of vars in the program
- terminates in O(|V||N|) time, where |N| is # of CFG nodes

algo. (using worklist to solve in[n])

initialize in[n] := ∅ for all n in CFG
initialize worklist w := all nodes in CFG
- invariant: node n's equations are not currently satisfied => n in w
while w is not empty:
1. w := w - {n}
2. in[n] := use[n] $\cup$ ( $\bigcup_{n'>n}$ in[n'] - def[n])
3. if in[n] changed:
  1. w := w $\cup$ {n': n' < n}

correctness:

invariant is proven by induction => equations are satisfied on termination => partial correctness
terminates O(|N||V|) time

eg. we can use this to detect dead assignments:

while (z < 1000) {
    int y = 100;
    if (z > 10) {
        return y;
    } else {
        y = z;
        z = z + 1;
    }
}
int y = z;
return y;

the statement y = z is a dead assignment.

eg. by jls 14.20 all statements must potentially execute

f();  // reachable only if f() terminates (unreachable)
x = y + 1;
return;
if (x > 1) {...}  // cannot potentially execute

Week 8. Feb 28

reachable statement analysis

the CFG will be all joos statements (same graph) + 2 synthetic nodes: start and end.

eg.

int f(int x) {
    while (g(x) > 0) {
        S;
    }
    return 0;
}

the CFG is:

if we change while (g(x) > 0) to while (1>0), then the edge labelled F is gone. the return statement is now unreachable. if we change it to while (1<0), then the edge labelled T is gone, S is unreachable.

specially, JLS says if-else conditions are not treated as constants for reachability purposes

justification: so that programmer can flip conditions for debug
although constant folding can be done for optimization

to compute reachability, we define

in[n] = true iff program point before n may be reached
- in[n] = $\bigvee_{n'<n}$ out[n']
- compiler needs to report error of in[n] = false
- in[start] is always true
out[n] = true iff program point after n may be reached
- out[n] = false if n is return; or return e;
- out[n] = true if n is start
- out[n] = in[n] otherwise

this is a forward analysis (info propagates from start node), while the liveness analysis is a backward analysis.

algo. (computing out[n] with iterative solving)

initialize out[n] := false for all n in CFG
repeat until no changes to out[n]:
1. out[n] = the formulas

algo. (computing out[n] with worklist)

initialize out[n] := false for all n in CFG
set worklist w := all nodes in CFG
while w is not empty:
1. w = w - {n}
2. out[n] = the formulas
3. if out[n] changed:
  1. w = w $\cup$ {n': n' > n}

eg. LJS also requires if method return type is not void, then every finite execution path must return.

int f(int x) {
    if (x > 0) {
        return 1;
    }
    // need to error
}

we look at in[end]. if it is true, then we are missing a return statement.

this is because we always set out to be false for return nodes, and in[end] is the union of end's predecessors' outs.

available copies analysis

eg.

y = f(0);
x = y;
...
z = 3 * x;

we can know y is copied over to the assignment of z. then we can convert the code to

y = f(0);
...
z = 3 * y;

define some auxiliary functions:

n	`gen[n]`	`kill[n]`
x <- y	{x=y}	{∀z:x=z} ∪ {∀z:z=x}
x <- e	∅	{∀z:x=z} ∪ {∀z:z=x}
[e1] <- e2	∅	∅
if e	∅	∅
return	∅	∅
start	∅	all available copies

define

in[n] = available copies before n executes ({x1=y1, ..., xn=yn})
- in[n] = $\bigcap_{n'<n}$ out[n']
out[n] = available copies after n executes
- out[n] = gen[n] ∪ (in[n] - kill[n])

this is also a forward analysis, we can use same worklist algo.

dataflow analysis framework

in summary:

	top	transfer function	meet operator
LVA (backward)	∅	`in[n] = use[n] ∪ (out[n] - def[n])`	`out[n] =` $\bigcup_{n'>n}$ `in[n']`
RSA (forward)	false	`out[n] = ...`	`in[n] =` $\bigvee_{n'<n}$ `out[n']`
ACA (forward)	all copies	`out[n] = gen[n] ∪ (in[n] - kill[n])`	`in[n] =` $\bigcap_{n'<n}$ `out[n']`

dataflow analysis framework:

L = space of facts (dataflow values)
- for LVA, it is set of live vars
- for RSA, it is true/false
- for ACA, it is set of available copies
- ℓ ∈ L: fact about a program point in CFG
direction = forward or backward
how CFG nodes transform the facts:
- forward: out[n] = Fn(in[n])
- backward: in[n] = Fn(out[n])
meet operator ∏:
- forward: in[n] = $\prod_{n'<n}$ out[n']
- backward: out[n] = $\prod_{n'>n}$ in[n']
top element in L: maximal info in the space of facts
- is the least conservative option

the worklist algo does not specify in which order to remove n from worklist, so it can be inefficient if CFG has cycles.

we can first find all strongly connected components in the CFG, then do a topo sort on the SCCs
so we can do a single traversal in this order => more efficient
there might still be cycles in SCCs, but they are smaller

algo. (iterative solving for forward analysis)

initialize out[n] := top for all n in CFG
repeat until convergence:
1. for each node n:
  1. out[n] = $F_n\left(\prod_{n'\prec n}\texttt{out[n']}\right)$

iterative solving

claim: iterative approximation = computing a fixed point.

given N nodes in CFG, start from $(T,T,...,T)\in L^N$ , result is $(\ell_{n_1},...,\ell_{n_N})\in L^N$ . we use a single transfer function $F:L^N\to L^N$ with

F(\ell_{n_1},...,\ell_{n_2})=\left(F_{n_1}\left(\prod_{n'\prec n_1}\ell_{n'}\right),...,F_{n_N}\left(\prod_{n'\prec n_N}\ell_{n'}\right)\right)

algo. (iterative solving)

init X := (T, ..., T)
repeat until convergence:
1. X = F(X)

we need some conditions to ensure convergence and correctness:

claim. L must be a partial order (a set with a binary relation $\leq$ )

satisfies relations:
- reflexive: $\ell\leq\ell$
- transitive: if $\ell_1\leq\ell_2$ and $\ell_2\leq\ell_3$ , then $\ell_1\leq\ell_3$
- antisymmetric: if $\ell_1\leq\ell_2$ and $\ell_2\leq\ell_1$ , then $\ell_1=\ell_2$
$\ell_1\leq\ell_2$ $ℓ_{1} \leq ℓ_{2}$ means $\ell_2$ $ℓ_{2}$ is at least as informative as $\ell_1$ $ℓ_{1}$
- LVA: $\ell_1\leq\ell_2$ iff $\ell_1\subseteq\ell_2$
- RSA: $\texttt{true}\leq\texttt{false},\texttt{false}\leq\texttt{false},\texttt{true}\leq\texttt{true}$
- ACA: $\ell_1\leq\ell_2$ iff $\ell_1\subseteq\ell_2$

eg. for any set S, $(2^S,\subseteq)$ is a partial order.
we can use hasse diagram for S={a,b,c} case:

the height is 3.

eg. if $(L,\leq)$ is partial order, then $(L,\geq)$ is also a partial order.

claim. L must be a lower semilattice (partial order + GLB operator $\sqcap$ ).

+two requirements
1. lower bound: $\ell_1\sqcap\ell_2\leq \ell_1,\ell_1\sqcap\ell_2\leq\ell_2$
2. greater: $\forall \ell_3,\ell_3\leq\ell_1\land\ell_3\leq\ell_2\implies\ell_3\leq\ell_1\sqcap\ell_2$
LVA: $\sqcap=\cup$ ; RSA: $\sqcap=\vee$ ; ACA: $\sqcap=\cap$

claim. (condition 1): L must be a bounded lower semilattice (lower semilattice + top element).

+requirement on T: $\forall\ell\in L,\ell\leq T$

notation.

$(\ell_1,...,\ell_N)\leq(\ell_1',...,\ell_N')$ iff $\ell_i\leq\ell_i'$ for all i
$(\ell_1,...,\ell_N)\sqcap(\ell_1',...,\ell_N')=(\ell_1\sqcap\ell_1',...,\ell_n\sqcap\ell_N')$
$T\in L^N=(T,...,T)$

claim. if L is PO/semilattice/bounded semilattice, then so is $L^N$ .

the iterative solving then says given $X_0=(T,...,T)$ , we have $X_{i+1}=F(X_i)=F^2(X_{i-1})=...=F^{i+1}(X_0)$ . if it converges in k-th iteration, then we should have $X_{k+1}=F(X_k)=X_k$ .

eg. L={true, false}, <= is not more informative, F(l)=¬l. what if we apply iterative solving? it never converges. so we need more condition on tranfer function.

claim. (condition 2) F must be monotone, ie $\ell_1\leq\ell_2\implies F(\ell_1)\leq F(\ell_2)$ .

eg. Fn(l) = use[n] ∪ (l - def[n]) is monotone. it is also true $F:L^N\to L^N$ is also monotone.

eg. suppose we want to find the fixed point of transfer function F.

we first apply F to x0, then apply F to x1 and so on until we approach a fixed point xk. our algo then terminates.

what if we have a transfer function that is not bounded below:

it will descend forever.

claim. (condition 3) L must be of finite height.

$\ell_0>\ell_1...>\ell_k>...$
L has height h => $L^N$ has height Nh.

we can use this to prove termination of iterative solving. if we know $X_1\leq X_0$ , then by transitivity and condition 2 we know $X_2=F(X_1)\leq F(X_0)=X_1$ ... using inductive argument we can prove that $X_{i+1}\leq X_{i}$ for all i. by condition 3, there must exist a k such that $X_0\geq X_1\geq X_k=X_{k+1}$ where $k\leq Nh$ .

so blindly applying the transfer function Nh times we will get a fixed point.

next we want to show $F^{Nh}(T)$ is the greatest fix point, ie $X=F(X)\implies X\leq F^{Nh}(T)$ . we know $X\leq T$ , then $X=F(X)\leq F(T)\leq F^2(T)\leq...\leq F^{Nh}(T)$ .

in summary, if L is bonded lower semilattice + top + finite height, F is monotone, then iterative solving will give best fixed point in Nh iterations.

Week 9. Mar 7

IR

source -> AST (with optimization) -> IR (can have high level IR, middle level IR, low level IR) -> machine code

IR design goals

simplicity
language independence
machine independence
support optimization + codegen

approaches:

low-level AST IR with mem ops and jumps (TIR, appel's)
stack-based IR (JUM, wasm)
- easy to generate code/interpret IR code
- harder to do optimizations (less like asm language)
3-address code. quadruples (llvm)
- x1 <- x2 op x3
- no subexpressions => easier to do analysis
- harder to do intruction selection
A-norm ≈ 3addr code + higher order control
- pass lambda around
- (functional languages)

TIR	IR node type	abbreviation
`Expression e ::=`	`CONST(n)`	`n`	literal(any type)
	`TEMP(t)`	`t`	assume infinite supply of temps
	`OP(e1, e2)`	`e1 op e2`	binary op
	`MEM(e)`		memory at
	`CALL(` $e_f,\vec{e}$ `)`		$e_f$ is addr of code
	`NAME(l)`		l is a code/data label
	`ESEQ(s, e)`	`s;e`	do statement s, then evaluate e
`OP ::=`	`ADD\|MUL\|SUB\|DIV` `MOD\|AND\|OR\|XOR` `NOT\|RSH\|LSH\|ASH` `EQ\|NEQ\|LT\|GT` `LE\|GE`
`Statement S ::=`	`MOVE(` $e_{\text{dst}},e$ `)`		$e_{\text{dst}}$ `::= TEMP(t) \| MEM(e)`
	`EXP(e)`		evaluate e, discard result
	`SEQ(` $\vec{s}$ `)`	`s1;...sn;`
	`JUMP(e)`		e is address
	`CJUMP(e, l1, l2)`		eval e, if 0 then jump to l1, else to l2
	`LABEL(l)`		naming current program point
	`RETURN(e)`

interpreting TIR: post-order traversal on IR AST except at c|jump/call/return.

/u/cs444/pub/tir

translating from source language to IR

we have two mutually recursive functions:

E[[e]] = e': takes source expression and returns IR expressions
S[[S]] = S': takes source statement and returns IR statement

expression:

E[[n]] = CONST(n)
E[[true]] = CONST(1)
E[[false]] = CONST(0)
E[[e1 + e2]] = OP(E[[e1]], E[[e2]])
E[[x]] = TEMP(x)
E[[f(e1, ..., en)]] = CALL(NAME(f), E[[e1]], ..., E[[en]])

translating function:

F[[τ f(τ1 x1, ..., τn xn) {s}]] =
  LABEL(f);
  MOVE(TEMP(x1), TEMP(ARG1));
  ...
  MOVE(TEMP(xn), TEMP(ARGn));
  S[[s]];

statements:

S[[int x = e;]] = MOVE(TEMP(x), E[[e]])
S[[s1; ...; sn]] = SEQ(S[[s1]], ..., S[[sn]])
S[[if(e) s]] = SEQ(CJUMP(E[[e]], lt, lf); LABEL(lt); S[[s]]; LABEL(lf))
- shorthand:
```
CJUMP(E[[e]], lt, lf);
lt: S[[s]];  ; fresh labels
lf:
```
S[[return e]] = RETURN(E[[e]])

logical and (with shortcircuit):

E[[e1 && e2]] = /*ESEQ(SEQ(*/
  MOVE(t, 0);
  CJUMP(E[[e1]], lt, lf);
  lt: MOVE(t, E[[e2]]);
  lf:/*)*/ TEMP(t)/*;)*/

eg. how to translate S[[if (e1 && e2) s]]? can compose two translations above

CJUMP(ESEQ(SEQ(...), TEMP(t)), lt, lf)
lt: ...
lf: ...

there are fragmented branches => inefficient. we can do

CJUMP(E[[e1]], l, lf);
l: CJUMP(E[[e2]], lt, lf);
lt: S[[s]]
lf: ...

we define C[[e, lt, lf]] = IR stmt that jumps to lt if e is nonzero:

C[[true, lt, lf]] = JUMP(lt)
C[[false, lt, lf]] = JUMP(lf)
C[[!e, lt, lf]] = C[[e, lf, lt]]

C[[e1 && e2, lt, lf]] =
  C[[e1, l, lf]];
  l: C[[e2, lt, lf]]

C[[e1 || e2, lt, lf]] =
  C[[e1, lt, l]];
  l: C[[e2, lt, lf]]

when we have this, then we can easily translate the if statement:

S[[if (e) S]] =
    C[[e, lt, lf]]
    lt: S[[S]]
    lf: ...

translating while:

C[[while (e) s]] =
  lw: C[[e, lt, lf]]
    lt: S[[s]]
        JUMP(lw)
    lf: ...

arrays

we represent arrays as sequence of 4-byte words

int[] a = new int[n];

+-----------+
|  length   |
+-----------+
|  vtable   | <- TEMP(a)
+-----------+
|   a[0]    |
+-----------+
|   ....    |
+-----------+
|  a[n-1]   |
+-----------+

translating indexing:

E[[e1[e2]]] =
  MOVE(ta, E[[e1]])
  CJUMP(EQ(ta, 0), l_err, l_nn)  // check for null
  l_err: CALL(NAME(__exception)) // lib function
  l_nn: MOVE(ti, E[[e2]])
  CJUMP(LTU(ti, MEM(ta - 4)), l_ib, l_err)  // unsigned lt
  l_lb: MEM(ta + ti * 4 + 4)

translating assignment to array element:

E[[e1[e2] = e3]] =
  MOVE(ta, E[[e1]])
  // check for null
  MOVE(ti, E[[e2]])
  // check for bounds
  MOVE(te, E[[e3]])
  MOVE(MEM(ta + ti * 4 + 4), te)
  te

translating new array:

E[[new int[e]]] =
  MOVE(tn, E[[e]])
  // check nonnegative
  MOVE(tm, CALL(NAME(__malloc), tn * 4 + 8))
  MOVE(MEM(tm), tn)  // store length
  MOVE(MEM(tm + 4), ...)  // store vtable
  // loop to store arr elements which are 0-initialized
  TEMP(tm + 4)

IR lowering

what are different from assembly:

deep trees of nested expressions/statements => >=1 side effects per statement
calls as expressions
two-way jumps

plan:

flatten all SEQs and ESEQs into a toplevel SEQ
- no nested statements
- expr cannot have side effects
- one side effect per statement
CALLs become statements
CJUMP's false branch becomes fall through

we will have lowered IR:

code ::= SEQ(s1, ..., sn)
   s ::= MOVE(e_dst, e)   e_dst ::= MEM(e) | TEMP(t)
         JUMP(e)
         CJUMP(e, l)  // deal later
         LABEL(l)
         RETURN(e)
         CALL(e_f, ...e)
   e ::= CONST(n) | TEMP(t) | OP(e1, e2) | MEM(e) | NAME(l)

we have function:

L[[e]] = $\vec{s}$ $s$ | e' (TIR expr => LIR stmt and a pure LIR expr)
- pure: either const, temp or label
- we separate side effects and results
L[[S]] = $\vec{s'}$ (TIR stmt => LIR stmt)

translating statements:

L[[LABEL(l)]] = LABEL(l)
L[[SEQ(s1, ..., sn)]] = L[[s1]]; ...; L[[sn]]
L[[JUMP(e)]] = $\vec{s}$ ; JUMP(e') given L[[e]] = $\vec{s}$ | e'
L[[CJUMP(e, l1, l2)]] = $\vec{s}$ ; CJUMP(e', l1, l2) given L[[e]] = $\vec{s}$ | e'
L[[EXP(e)]] = $\vec{s}$ given L[[e]] = $\vec{s}$ | e'
L[[RETURN(e)]] = $\vec{s}$ ; RETURN(e') given L[[e]] = $\vec{s}$ | e'

expressions:

L[[e]] = |e if e is pure
L[[MEM(e)]] = $\vec{s}$ | MEM(e') given L[[e]] = $\vec{s}$ | e'
L[[ESEQ(s, e)]] = $\vec{s'}$ ; $\vec{s''}$ | e' given L[[s]] = $\vec{s'}$ and L[[e]] = $\vec{s''}$ | e'
L[[OP(e1, e2)]] = $\vec{s_1}$ $s_{1}$ ; $\vec{s_2}$ $s_{2}$ | OP(e1', e2') given L[[e1]] = $\vec{s_1}$ $s_{1}$ | e1' and L[[e2]] = $\vec{s_2}$ $s_{2}$ | e2'
- use only if $\vec{s_2}$ and e1' commute
L[[OP(e1, e2)]] = $\vec{s_1}$ $s_{1}$ ; MOVE(tm, e1'); $\vec{s_2}$ $s_{2}$ ; | OP(t, e2')
- fallback rule
L[[CALL(e0, e1, ..., en)]] = $\vec{s_0}$ $s_{0}$ ; MOVE(t0, e0'); ...; $\vec{s_n}$ $s_{n}$ ; MOVE(tn, en'); CALL(t0, t1, ..., tn); TEMP(ret) given L[[ei]] = $\vec{s_i}$ $s_{i}$ | ei' for all i
- ret ~ eax

translating move:

L[[MOVE(TEMP(t), e2)]] = $\vec{s}$ ; MOVE(t, e2') given L[[e2]] = $\vec{s}$ | e2'
L[[MOVE(MEM(e1), e2)]] = $\vec{s_1}$ ; MOVE(t, e1'); $\vec{s_2}$ ; MOVE(MEM(t), e2') given L[[e1]] = $\vec{s_1}$ | e1' and L[[e2]] = $\vec{s_2}$ | e2'

when can we know side effects in $\vec{s_2}$ cannot affect $e_1'$ ?

if $\vec{s_2}$ $s_{2}$ assigns into temp that is read by $e_1'$ $e_{1}^{'}$
- $\vec{s_2}$ writes TEMP(t3) and $e_1'$ reads TEMP(t4), only check t3 != t4
if $\vec{s_2}$ $s_{2}$ assigns into mem read by $e_1'$ $e_{1}^{'}$
- $\vec{s_2}$ writes MEM(t3) and $e_1'$ reads MEM(t4). whether e3 and e4 are same address is undecidable
- heuristics:
  - e3 and e4 are translations of joos expressions of different types
  - e_3 = t + n, e_4 = t + m where immediates n != m
  - generally want pointer analysis & SMT solver

Week 10. Mar 14

canonicalizing cjumps

one idea: CJUMP(e, l1, l2) = CJUMP(e, l1); JUMP(l2)

more jumps => code is inefficient

new idea: reorder code so that l2 is always next statement

need to introduce new concepts:

ordinary statement: -> S -> S'
jump statement:
```
-> jump -> S'
    |
    v
   ...
```
return statement
```
-> ret    S'
```
labels:
```
-> l: -> S'
   ^
   |
  ...
```

defn. a basic block is a sequence of statements s1, ..., sn such that:

all but s1, sn are ordinary statements
s1 can be orinary or jump statement
sn can be ordinary or jump/ret statement

basic block either executes fully or not at all.

a maximal basic block is a basic block that cannot be extended to a larger basic block.

defn. the trace in a CFG is sequentially distinct basic blocks.

algo. (greedy reordering)

init all blocks as unmarked
repeat until all blocks are marked:
1. choose an unmarked block
2. mark a maximal unmarked trace from the block
3. append blocks in this trace to output (while fixing/simplifying jumps)
  1. delete jumps to next bb
  2. invert cjumps as needed; drop arg
  3. append jump to bb as needed
  4. delete unneeded labels

eg. given

l0:  CJUMP(e, l2, l3)
l1:  MOVE(x, y)
l2:  MOVE(x, y + z)
     JUMP(l1)
l3:  CALL(f)
     RETURN

we build a CFG on this where vertices are basic blocks:

l0 -> l2 <-> l1
   \
    v
    l3

l0->l2->l1, l1->l2, l0->l3 are traces.

consider l0->l2->l1, steps:

delete jump(l1)
invert top cjump
add jump below l1

then we do 2nd iteration to handle unmarked l3

- l0: CJUMP(e, l2, l3)
+ l0: CJUMP(!e, l3)
  l2: MOVE(x, y + z)
-     JUMP(l1)
  l1: MOVE(x, y)
+     JUMP(l2)

  l3: CALL(f)
      RETURN

heuristics for picking traces:

prefer traces without unmarked predecessor
perfer hot code and hot edges
- profiling
- back edges (loops) take priority over forward edges
ML models

instruction selection

we generate almost assembly code except we assume there are infinitely many registers.

steps:

cover AST with tiles
add abstract registers between tiles
emit code bottom-up

eg. instruction selection as tiling

MOVE(t1, t1 + MEM(t2 + 8))

result:

move t3, t2
;
mov t4, t3
add t4, 8
;
move t5, [t4]
;
add t1, t5

the whole tree can be viewed as one tile, and we get

add t1, [t2 + 8]

questions:

what instructions are there?
what can be a tile (pattern to match ast)?
how to select tiles?

x86 ISA

intel 4040    ->    intel 8080    ->    intel i386    ->    amd64
- 8bit addr         - 16bit addr        - 32bit addr        - 64bit addr
                    - 8 8bit gpr        - 8 32bit gpr       - 16 64bit gpr

2-address usc isa:

instruction has form opcode dest, src[, src] (intel syntax)
opcodes: and, or, xor, not, shr, shl, sar, add, sub, mul, div, inc, dec, cmp, test, mov, push, pop, call, ret, ...
general purpose registers: eax, ebx, ecx, edx, esi, edi, esp, ebp
- for the first four registers, the [8:0] bits can be accessed as al, bl, cl, dl, the [15:8] bits can be accessed as ah, bh, ch, dh, the [31:16] bits can be accessed as ax, bx, cx, dx
- esp is reserved as stack pointer
operands
- const: 17 (CONST(17))
- reg: eax (TEMP(eax))
- mem addr: [eax + ebx * 4 - 3] (MEM(eax + ebx * 4 - 3))
  - in general: addr is base + index * scale + offset
    - base, index are registers, scale is 1, 2, 4, 8, offset is const

size inference and directives

add eax, [ebx]  // inferred as 32 bit
inc dword [ebx] // need to specify (byte-8, word-16, dword-32)

only one memory operand is allowed per instruction.

branching instruction:

cmp ebx, ecx
jz l1  // if condition code is zero, jump to l1 
je l1  // equal
jl l1  // less (also jnge)
jnz l1

condition codes are set by cmp, test, xor, ... and tested by jcc/setcc.

setz al // set lower 8 bit

tiling is not syntax-direct translation, but pattern matching.

we define

T[[e]] t = instruction sequence that puts result of IR expression e into assembly register t
T[[s]] = instruction sequence that computes IR statement s

some patterns:

T[[MOVE(t, 0)]] = mov t, 0 or xor t, t
T[[ADD(t1, t2)]] t3 = lea t3, [t1 + t2]
T[[ADD(k, ADD(e1, MUL(e2, w)))]] t = where w=1,2,4,8
```
T[[e1]] t1
T[[e2]] t2
lea t, [t1 + t2 * w + k]
```

T[[EQ(e1, e2))] t =

T[[e1]] t1
T[[e2]] t2
cmp t1, t2
setz al
movzx t, eax // clears high bits of eax & move eax to t

T[[CJUMP(e, l)]] =
```
T[[e]] t
test t, t
jnz l
```
T[[CJUMP(EQ(e1, e2), l)]] =
```
T[[e1]] t1
T[[e2]] t2
cmp t1, t2
jz l
```

tiling algorithms:

algo. (greedy): choose tiles greedily by priority size of tile

match root if ir ast with highest-priority matching tile
recursively match subtrees

eg.

the result is

mov t1, [t2 + 8]
mov t2, [t + 7]
mov [t1 + t2 * 4], 3

good: no search => fast. bad: not optimal.

assume there is a notion of optimality: cost of tiling a tree using a tile = cost of the tile + cost of tiling the subtrees, we also can have bellman equations:

\mathrm{cost}(tr)=\min_{tile}\left(\mathrm{cost}(tile)+\sum_{\substack{tr'\text{ is subtree of }tr\\\text{ after covering with tile}}}\mathrm{cost}(tr')\right)

algo. (dynamic programming)

use optimal tiling if memoized already
for each tile matching the root of tree
1. recursively tile subtrees
2. compute cost of tiling
memoize best tiling and its cost

runtime: O(nt) where n is # of nodes in tree and t is # of matching tiles.

pros and cons:

+ general strategy for optimizing tiling
- expensive
- need a cost model

goals:

completeness => cover all asts
efficiency => leverage ISA (mem operand, rich addressing modes)

strategy:

first syntax-directed tiles
then add tiles to improve code quality

tiling call/return

an x86 call f is roughly equivalent to

sub esp, 4
mov [esp], eip  // push return addr onto stack
jmp f

calling convention:

cdecl (mainstream for x86)
first push arguments to stack in reverse order and return address
then result is returned in eax

before call                 pushing                 during call
           higher addr
|         |   ^           |          |             |           |
|         |   |           |          |             |           |
+---------+               +----------+             |           |
|         |  < esp        |          |             |           |
+---------+               +----------+             |           |
|         |               |   arg2   |             |           |
|         |               |   arg1   |             +-----------+
|         |   |           |caller eip| < esp       |caller ebp |
|         |   v           +----------+             +-----------+        ^
|         |stack grows    |          |             |   temp    |        | L
                                                   |  storage  | < esp  |
                                                   +-----------+        v

T[[CALL(f, e1, ..., en); MOVE(t, RET)]] =
  T[[en]] tn
  push tn     //   sub esp, 4
              //   mov [esp], t
  ...
  T[[e1]] t1
  push t1
  call f
  mov t, eax
  add esp, 4 * n

function prologue:

push ebp
mov ebp, esp
sub esp, 4 * L  // temps at [ebp-4*i]

function epilogue:

mov esp, ebp
pop ebp       // mov t, [esp]
              // add esp, 4
ret

caller-vs-callee-saved registers:

	caller	callee
caller-saved	must save value on stack restore after call	can use freely
callee-saved	can use freely	must save value on stack restore before return

caller-saved: eax, ecx, edx
callee-saved: esp, ebp, ebx, esi, edi

constant-size frame optimization

ebp = esp + 4*L => can avoid using ebp, ie [ebp + k] = [esp + k + 4 * L]
prologue: sub esp, 4 * L
epilogue: add esp, 4 * L; ret
dynamic stack allocation is not allowed

eg. C vla:

// int a[f()];
call f
shl eax, 2
sub esp, eax
mov a, esp

Week 11. Mar 21

register spilling

idea: put all abstract registers on stack, and access them using [ebp-4], [ebp-8], ...

observations: any given x86 instructions uses at most 3 registers => we reserve 3 registers.

eg.

push t
// translates to (t maps to ecx)
mov ecx, [ebp - kt]
push ecx

mov a, [b + 8]
// translates to (a maps to ecx, b maps to edx)
mov edx, [ebp - kb]
mov ecx, [edx + 8]
mov [ebp - ka], ecx

add x, y
// translates to (x maps to ecx, y maps to edx)
mov ecx, [ebp - kx]
mov edx, [ebp - ky]
add ecx, edx
mov [ebp - kx], ecx

sub [x + d * y + 31], z
// translates to (x maps to ecx, y maps to edx, z maps to eax)
mov eax, [ebp - kz]
mov ecx, [ebp - kx]
mov edx, [ebp - ky]
sub [ecx + 8 * edx + 31], eax

compiling OO features

memory layout:

fields placed sequentially
fields aligned to not cross word boundary
instruction pointers to methods are stored in dispatch vector

eg. in cpp

struct CPP {
    short x;    // 16 bits
    char y;     // 8 bits
    CPP *next;  // 32 bits
    virtual ~CPP() {}
}

memory:

MSB        LSB
+-----------+
|  header   |
+--+--+-----+
|  |y |  x  |
+--+--+-----+
|    next   |
+-----------+

eg. in joos

class Joos {
    short x;    // 16 bits
    char y;     // 16 bits
    Joos next;  // 32 bits
}

memory:

+-----------+         +-----------+
|  header   |         |  header   |
+-----+-----+         +-----+-----+
|  y  |  x  |   or    |     |  x  |
+-----+-----+         +-----+-----+
|    next   |         |     |  y  |
+-----------+         +-----+-----+
                      |    next   |
                      +-----------+

constructors: compiled like static methods except it allocates memory. "this" points to newly allocated memory.

method dispatch

method dispatch: compiled as function with extra argument for receiver

goals:

fast dispatch
low per-object overhead
code sharing (seperate compilation)

idea 1: smalltalk

objects points to 'class objects'
on a call, walk up class hierarchy, find first matching method in class object
pros: code sharing
cons: slow

idea 2: attach dispatch vectors (array of code pointers) to objects

pros: fast dispatch, code sharing, low per-object overhead
cons: only works for single inheritance

eg.

class Point {
    int x, y;
    void setX(int x) { this.x = x; }
    void moveX(int dx) { this.setX(x + dx); }
}

class ColoredPoint extends Point {
    Color c;
    void setX(int x) {
        this.x = x;
        c = Colors.redden(c);
    }
    Color getColor() { return c; }
}

Point p = new ColoredPoint();
p.setX(42);  // p gets redder
p.moveX(1);  // p gets more redder

Point:
+-----------+      +-------------+
|  header  ------->|    setX() -----------> Point:setX()
+-----------+      +-------------+
|    x      |      |    moveX() ----------> Point:moveX() <--+
+-----------+      +-------------+                           |
|    y      |                                                |
+-----------+                                                |
                                                             |
ColoredPoint:                                                |
+-----------+      +-------------+                           |
|  header  ------->|    setX() -----------> CP:setX()        |
+-----------+      +-------------+                           |
|    x      |      |    moveX() -----------------------------+
+-----------+      +-------------+
|    y      |      |  getColor() ---------> CP:getColor()
+-----------+      +-------------+
|    c      |
+-----------+

observatation: Point is a prefix of ColorPoint (prefix) => compiler can treat a ColorPoint as a Point => achieving code sharing.

// p.moveX(1)
MOVE(T_DV, MEM(p))
CALL(MEM(T_DV + 4), p, 1)
// translates to
mov tdv, [p]
push 1
push p
call [tdv + 4]

field access is done by offseting from object pointer

// p.x
MEM(p + 4)

note. for abstract classes, we do not need DV for instance, but still need DV layout and compiled code for non-abstract method.

code for assmebly:

// Point.s
section .text
global Point$$setX$I
Point$$setX$I:
    ...
global Point$$moveX$I
Point$$moveX$I:
    ...
global Point$$$
Point$$$:
    ...

// vtable for Point
section .data
global Point
Point:
extern java$lang$Object$$getClass$
dd java$lang$Object$$getClass$  // define dword at first 32 bits
extern java$lang$Object$$clone$
dd java$lang$Object$$clone$     // next 32 bits
extern java$lang$Object$$hashCode$
dd java$lang$Object$$hashCode$
extern java$lang$Object$$toString$
dd java$lang$Object$$toString$
extern java$lang$Object$$equals$Ljava.lang.Object
dd java$lang$Object$$equals$Ljava.lang.Object
dd Point$$setX$I
dd Point$$moveX$I

// ColoredPoint.s
section .text
global ColoredPoint$$getColor$
ColoredPoint$$getColor$:
    ...
global ColoredPoint$$setX$I
ColoredPoint$$setX$I:
    ...
global ColoredPoint$$$
ColoredPoint$$$:
    ...

section .data
global ColoredPoint
ColoredPoint:
extern java$lang$Object$$getClass$
dd java$lang$Object$$getClass$
extern java$lang$Object$$clone$
dd java$lang$Object$$clone$
extern java$lang$Object$$hashCode$
dd java$lang$Object$$hashCode$
extern java$lang$Object$$toString$
dd java$lang$Object$$toString$
extern java$lang$Object$$equals$Ljava.lang.Object
dd java$lang$Object$$equals$Ljava.lang.Object
dd ColoredPoint$$setX$I
extern Point$$moveX$I
dd Point$$moveX$I
dd ColoredPoint$$getColor$

what does java do: support dynamic loading of classes => no guarantee code is compiled

jvm computes offsets at load time

java:     cp.getColor()
               |   javac
               v
bytecode: invokeVirtual "CP.getColor"
               |   java
               v
          invokeVirtualQuick 2
            /               \ only 1 version (final)
jit:       v                 v
     mov tdv, [cp]         call getColor directly/inline
       ...
     call [tdv + 2 * 4]

interfaces

problem: class/interface can extend >= 1 interfaces and 1 class.

we have colliding method offsets

                    I1   DV = {a()}
                   /  \
                  /    \
DV = {a(), b()}  I2    I3 DV = {a(), c()}
                  \    /
                   \  /
                    C4 DV = {a(), b? c?}

idea 1: inline caching

used by smalltalk
insight: 90% of calls at call site go to same code
use cache in global data

assume line 444 has code o.m()

        |       |
ld444   |     -----> last class of o seen
code444 |     -----> last method m called
        |       |

the calling sequence is

L444: mov tid, [o]  // assume o points to class id, then fields
      cmp tid, [id444]
      jne miss444
      call [code444]
done444: ...
miss444:
      call slowDispatch
      mov [id444], tid
      mov [code444], methodptr
      jmp done444

cons: thread safety
- thread-local cache (has cost)
- pack id and code pointer into single word
widely used in dynamic languages

polymorphic inline caching: 2-4 entires of cache

idea 2: assign indices to not collide

eg.

interface Color {
    RGB rgb();
    HSV hsv();
}
interface Clickable {
    void click();

}
interface Shape {
    Box bounds();
}
class Graphics implements Shape, Color {
    Box bounds();
    RGB rgb();
    HSV hsv();
}
class Button implements Shape, Clickable {
    Box bounds();
    void click();
}

if we assign 0: rgb, 1: hsv, 2: click, 3: bounds, then we have wasted fields but they are compatible

Graphics DV: {rgb(), hsv(), 0, bounds()}
Button DV: {0, 0, click(), bounds()}

we can be smarter to assign 1: rgb, 2: hsv, 1: click, 0: bounds, then we have densely packed DVs

Graphics DV: {bounds(), rgb(), hsv()}
button DV: {bounds(), click()}

observation: two methods conflict if they are present in same class => can draw interference graphs

graph coloring = assigning indices
it is np-complete => can use heuristics
always can increase DV size

              rgb
             /  |
click -- bounds |
             \  |
              hsv

this approach requires whole-program info => cannot do seperate compilation.

idea3: compute indices by hashing

eg.

interface PointI {
    void setX(int x);
    void moveX(int dx);
}
class Point implements PointI {
    int x, y;
    void setX(int x);
    void moveX(int x);
}
interface Colored {
    Color getColor();
}
class ColoredPoint extends Point implements Colored {
    Color c;
    Color getColor();
}

IDT ~ hash table
$h_{setX}$ := precomputed hash for PointI.setX shared by all classes implementing PointI

calling sequence:

// PointI p = ColoredPoint();
// p.setX(6);
MOVE(t_CDV, MEM(p))
MOVE(t_IDT, MEM(t_CDV))
MOVE(t_setX, AND(h_setX, MEM(t)IDT))  // effectively h_setX = h_setX % 2^N
CALL(MEM(t_IDT + 4 * t_setX + 4), id_setX, p, 6)  // pass method id in case of collision

mov t_CDV, [p]
mov t_IDT, [t_CDV]
mov t_setX, h_setX
and t_setX, [t_IDT]
push 6
push p
push id_setX
call [t_IDT + 4 * t_setX + 4]

to dispatch interface methods, we need 8 instructions whereas for method we need 4.

first load also mostly like leads to cache miss (other three are shared objects)

tension: size N vs. hash collision rate

instanceof

o instanceof C;
C c = (c)o;
arr[i] = o;

idea1: use CDV as class identity; store in CDV a pointer to parent's CDV

EQ(MEM(o), t_CDV(C)) ||
EQ(MEM(MEM(o)), t_CDV(C)) ||
...

pros: caching; seperate compilation
cons: linear search for single inheritance, tree search for multiple inheritance

idea 2: assume class hierarchy depth <= 4,

reserve N words in CDV
ith slot points to ith ancestor

calling sequence:

// o instanceof Ci (assume Ci is ith class in C's hierarchy)
EQ(MEM(t_CDV(Ak) + 4 * i), t_CDV(Ci))

+ O(1) time
- O(MN) space where M is height of hierarchy and N is number of classes
- need to know N
- no multiple inheritance support

idea 3: use a global M*M table where M = number of types

Ti is a suptype of Tj iff table[i][j]
+ O(1) time
+ works for multiple inheritance
- O(M^2) space
- need to know M

Week 12. Mar 28

register allocation

eg.

                 // live analysis
                 // a
mov b, a         // b, a
mov c, [b * 4]   // c, a
lea b, [c + 1]   // a, b
mov d, a         // b, d
imul d, b        // d
mov eax, d       // eax
ret              //

we create CFG and use live var analysis backwards to get live sets.

obersavation: we have low register pressure:

<= 2 vars are live simultaneously
a, d are never live at same time
b, c are never live at same time

so we substitute a, b with eax; b, c with edx:

mov edx, eax
mov edx, [edx * 4]
lea edx, [edx + 1]
// mov eax, eax
imul eax, edx
// mov eax, eax
ret

observation:

if two vars are in the same live-out set, then they cannot be assigned to same register
we can coalesce movs
some regs are def'ed by instruction and var live-out from same instruction => cannot be assigned to same register
- eg. imul t multiplies eax and t and stores result in edx and eax => cannot assign edx to t even if it may be trashed

draw interference graph
vertices: vars & machine registers
edges: interference

c  ----  a  ----  b  ----  d
red     blue     red      blue

graph coloring is np-complete:

we can use heuristics
allowed to fail => still spill vars to stack

kempe's heuristic:

suppose k colors are available
low-degree nodes (< k neighbours): rest of graph colorable => node must be colorable
high-degree nodes (>= neighbours): no such guarantee

algo. (kempe)

if theare are <= k nodes in graph, then we are done
if there exists low-degree node
1. color rest of graph recursively
2. pick a color different from < k neighbours of this node

eg. k = 3

    b
  / | \
a   |  d
  \ | / \
    c -- e

first we exclude a and color rest of graph, then we exclude b and color the rest, then we color c,d,e with different colors (say c=blue, d=yellow, e= green). then we color b=green, a=yellow.

if there are no low-deg nodes, graph may or may not be colorable (eg K4 vs planar graph of 5 nodes).

algo. (optimistic coloring)

if theare are <= k nodes in graph, then we are done
if there exists low-degree node
1. color rest of graph recursively
2. pick a color different from < k neighbours of this node
otherwise:
1. pick a high-degree node
2. color rest of graph recursively
3. try to find a color that works
4. spill vars to stack if failure

how to spill:

perviously, we use 3 regs for shuffling things on/off stack, which increases reg pressure.
we can spill with fresh abstract regs and retry reg allocation

eg. suppose we have to spil t2 to ebp - 8:

add t2, t1
// becomes
mov t44, [ebp - 8]
add t44, t1
mov [ebp - 8], t44

t44 has short liveness range => generates less interference => easier to allocate regs.

x86 peculiarities

there are instructions that use regs in special ways:

imul: eax (use/def), edx (def)
jcxz/jecxz: ecx (use)
call: caller-save regs (def)
this means we have to add precolored nodes for machine regs
- add edges accordingly
- cannot cur pre-colored nodes in kampe's

vars live-out from call interfere with caller-save regs

must use callee-save regs for the vars live out from a call
so prefer caller-save regs for the vars not live-out from a call

`mov` coalescing

idea: can delete mov t1, t2 if t1 is assigned with r and t2 is also assigned with r.

 \          /              \      /
-- t1 ---- t2 --   ==>   --- t1/t2 ---
 /          \              /      \
     mov-
    related

but the result has higher degree and can fail graph coloring.

conservative coalescing: never create nodes with >= k high-degree neighbours

             ----
             ----       /
many low-deg ----  t1/t2    (k-1) hi-deg neighbours
    nodes    ----       \
             ----

algo. (chaitin's)

LVA and build interference graphs
chop off low-degree, non-mov-related nodes, and push them to a stack
- now all nodes are high-degree or mov-related
conservatively coalesce mov-related nodes
1. coalesced nodes may be non-mov-related => rerun from 2
  - all nodes are high-degree or mov-related
  - mov-related nodes cannot be conseratively coalesced
pick a mov-related node and mark it "non-mov-related" => rerun from 2
- all nodes are high-degree
optimistically color high degree nodes
1. choose a node, remove and push onto stack => may create low-deg nodes => rerun from 2
  - we have no nodes left in graph
pop nodes from stack and try coloring them
if failure, rewrite code to spill variables => code is now different => rerun from 1

it has near-optimal result in practice, but very expensive.

compiling FP features

first-class functions:

assigned to variables
passe to functions as args
returned as return value
constructued at runtime

challenges: higher-order function

fun addfun(n: int): int -> int {
    fun f(x: int): int {
        return x + n
    }
    return f
}
val inc: int -> int = addfun(1)
inc(5) // 6

function closure = code + env (aka static link)

+-----------+
| inc  code --------> f code
+-----------+
|      env  --------> n = ...
+-----------+

closure conversion: convert free var access to env accesses

fun f(env: f.env, x: int): int {
    return x + env.n
}

inc.code(inc.env, 5)

envs are ideally on stack, in general on heap.

eg.

fun twice(f: int -> int): int -> int {
    fun g(x: int): int {
        return f(f(x))
    }
    return g
}
fun double(n: int): int {
    fun addn(x: int): int {
        return x + n
    }
    val addnTwice: int -> int = twice(addn)
    return addnTwice(0)
}
double(8)

first need to do closure conversion:

fun twice(f: f_clos) {
    val g = create g closure
    return g
}

// hoist g
fun g(env: g_env, y: int) {
    val f = env.f
    return f.code(f.env, f.code(f.env, y))
}

fun double(n: int): int {
    val addn = create f closure
    val addnTwice = twice(addn)
    return addnTwice.code(addnTwice.env, 0)
}

// hoise addn
fun addn(env: addn_env, x: int) {
    return x + env.n
}

call sequence/tree:

      double
  1 /     2 \
twice    addnTwice(=g)
         3 /    4 \
        addn(=f) addn(=f)

when call reaches twice:

when call leaves twice and reaches addnTwice:

envs point to lexically enclosing func's activation => static link chains

control flow is implicitly represented by stack pointer (not part of program)

CPS transformation

another approach: compiling with continuations

contiuation-pass style (CPS): control flow explicit as continuation closures
first convert program to CPS, then do closure converstion
result program can compile and run without stack

notations:

[[v]] k = e in CPS form, k is continuation function
- v ::= n | x | fun(x1, ..., xn) {e} | halt (value)
[[e]] k = e (expr) in CPS form
- e ::= v | v0(v1, ..., vn) | v1 + v2 | let x = v in e | ...
[[s]] k = s (stmt) in CPS form
- s ::= e | if v then s1 else s2 | s1; s2 | let x = v in s | ...

transformations:

[[n]] k = k(n)
[[x]] k = k(x)
[[e1 + e2]] k = [[e1]] (fun x1 => [[e2]] (fun x2 => let x = x1 + x2 in k(x)))
[[if (e) then s1 else s2]] k = [[e]] (fun x => if x then [[s1]] k else [[s2]] k)
[[s1; s2]] k = [[s1]] (fun _ => [[s2]] k)
[[fun(x1, ..., xn){e}]] k = k(fun(x1, ..., xn, k'){[[e]] k'}) where k' is return addr
[[e0(e1, ..., en)]] k = [[e0]] (fun x0 => [[e1]] (fun x1 => ... [[en]] (fun xn => x0(x1, ..., xn, k)) ...))

eg.

[[1 + 2]] halt =
    (fun x1 => (fun x2 => let x = x1 + x2 in halt(x))) 2 1

[[inc(1 + 2)]] halt =
    (fun f => (fun x1 => (fun x2 => let x = x1 + x2 in f(x, halt)) 2) 1) inc

note all function calls are now tail calls => we do not need call stack or setting up call frames

...
// call f
// ret
jmp f

cost: many 1st class functions (on heap) => gc overhead.

Week 13. Apr 4

constant propagation (with cond branches)

many important optimizations in single pass

const folding
const propagation
identify unreachable code

CPCB as dataflow analysis:

D = forward
L = info about each var and unreachability
- var info can be decomposed into components, each var is one component
  - L_x = {Top (T), Bottom (⊥)} ∪ Z
    - T: var value is arbitrary (undefined/unreachable at the program point)
    - Z: var is constant
    - ⊥: var may take multiple values
    - lattice of height 2
  - meet function ∏:
    - c ∏ T = c
    - c ∏ ⊥ = ⊥
    - c1 ∏ c2 = ⊥ if c1 != c2
    - c ∏ c = c
- L = true|false × Lx × Ly × ...
- ℓ = (unreachable?, (lx, ly, lz, ...)) ∈ L, lx, ... ∈ Lx
- top element T = (true, (T, T, T, ...))
- partial ordering: componentwise
- meet operator: componentwise (note multiple constants becomes bottom)

eg.

transfer function Fn(b, (v1, ..., vn)):

Fn(true, (...)) = (true, (T, ..., T))
Fn(false, (v1, ..., vn)) = (false, (v1', ..., vn')), where
- if node is not assignment xi <- e, then vi' = vi
- otherwise vi' = abstract interpretation of e using $\vec{v}$ $v$
  - ie try to evaluate e. eg ⊥+1=⊥, ⊥*0=0

eg. why do we not define lattice for Lx this way:

it has infinite height. consider code

int x = 0;
while (true) x = x + 1;

at each iteration, we might have {0}, {0,1}, ..., iterative solving will not finish.

note. the meet operator is not distributive on this transfer function (unlike previous ones), ie F(l1 ∏ l2) != F(l1) ∏ F(l2).

eg.

+--------+     +--------+
| x = 1  |     | x = 2  |
| y = 2  |     | y = 1  |
+--------+     +--------+
    |              |
+---v----+     +---v----+
| t=x+y  |     | t=x+y  |
+--------+     +--------+
(false,(1,2,3)) ∏ (false,(2,1,3)) = (false, (⊥,⊥,3))

         +--------+     +--------+
         | x = 1  |     | x = 2  |
         | y = 2  |     | y = 1  |
         +--------+     +--------+
(false,(1,2,T)) \        / (false,(2,1,T))
              +--v--∏---v-+ (false,(⊥,⊥,T))
              |  t = x+y  |
              +-----------+
              (false,(⊥,⊥,⊥))

abstract interpretation

it is semantic foundation of dataflow analyses.

two worlds:

concrete computations operates on concrete values $v\in\Z$
abstract computations on abstract values $\tilde{ v}\in L$

concrete world	abstract world
$v_1+v_2$	$\tilde{ v}_1+\tilde{v}_2$
$f_n(v)$	$F_n(\tilde{v})$

defn. suppose we have a concretion function $\gamma:L\to2^\Z$ , abstract interpretation is sound if, for all $\tilde{v}\in L$ and all $v\in\Z$ , if $v\in\gamma(\tilde{v})$ , then $f_n(v)\in\gamma(F_n(\tilde{ v}))$ .

notation. abstraction function is $\alpha:=\gamma^{-1}$ .

requirements:

$\alpha,\gamma$ $α, γ$ are monotone:
- $S_1\leq S_2\implies\alpha(S_1)\leq\alpha(S_2)$
- $\tilde{v}_1\leq\tilde{v}_2\implies\gamma(\tilde{v}_1)\leq\gamma(\tilde{v}_2)$
$\gamma$ is sound: $\gamma(\alpha(S))\leq S$
$\gamma$ is complete (optimal): $\tilde{v}\leq\alpha(\gamma(\tilde{v}))$

given $\alpha$ , the most precise $\gamma$ is

\gamma(\tilde{v})=\prod_{\tilde{v}\leq\alpha(S)}S=\bigcup_{\tilde{v}\leq\alpha(S)}S

there are more complex abstractions:

range of values (cubical abstraction)
polyhedral abstractions (ML)
sign/pairing
nullability of pointers and memory locations (pointer analysis)

static single assignment

SSA: every var has exactly 1 def.

eg. it is easy for straight line CFGs

x = 2         x1 = 2
  v
y = f(x)      y = f(x1)
  v
x = y         x2 = y
  v
z = x * 2     z = x2 * 2

eg. it is hard for general CFG

     x = 0
       v
+-> if x < 0
|   /      \
+ x=x+1    y=x

we use φ-assignment

     x1=0
       v
+-> x3=φ(x1,x2)
|      v
|   if x3 < 0
|    /       \
+ x2=x3+1    y=x3

why SSA: simplifies snalyses/optimizations.

if we do LVA, we can store all uses of a var at var's def
- x is live = x's use set is not empty
if we do const propagation, then it is just replacing each use of x with c
dead code elimination:
- without it, have to repeat analysis (eg x=0;y=x;, if y is dead, then have to do another analysis to find x is dead)
- with SSA, after removing y, update x's use set

conversion

key problem: where to insert φ-assignments.

defn. (path convergence criterion)

there are $n_1\neq n_2$ that both def x
there are proper paths $n_1\rightarrow*m,n_2\rightarrow*m$
the two paths are disjoint except at $m$
the two paths do not def x except at $n_1,n_2$

(m is the earliest place where two paths meet, and we want to insert phi here)

the arity of φ is the number of converging defs.

defn. in a CFG, node A dominates node B if A is on every path from Start to B.

it is reflexive: A dom A
it is transitive: A dom B ∧ B dom C => A dom C
it is antisymmetric: A dom B ∧ B dom A => A=B

so it is a partial order: A dom C ∧ B dom C => A dom B ∨ B dom A, hasse diagram is tree-like.

eg.

dominator analysis as dataflow analysis:

formula: A dom B <=> A = B ∨ A dom predecessors(B)
facts: out[n]: set of nodes dominating n
- out[n] = {n} ∪ $\bigcup_{n'\prec n}$ out[n']
- out[Start] = {Start}
L = all subsets of nodes
D: forward
Fn(l) = {n} ∪ l
meet operator: ∏=∪
Top T = all nodes

defn. m is in the dominance frontier DF(n) if

n does not strictly dominate m
n dominates a predecessor of m

we assume Start def's all vars.

eg. DF(E) = G. DF(A) = {A, G, Exit}. DF(D) = {A, Exit}.

algo. (iterative dominance frontiers for x)

let S := set of nodes containing defs of x
let $DF_0=\varnothing$
while DF changes:
1. $DF_{i+1}=DF(DF_i\cup S)=\bigcup_{n\in DF_i\cup S}DF(n)$

we find a fixed point x = DF(x ∪ S). we insert φ-assignments for variable x at these nodes.

how to find DF(n)? observation: let m be a node not strictly dominated by n, then m ∈ DF(n)

iff m has a predecessor dominated by n (defn.)
iff either m is a direct successor of n, or m is in DF(n') where n' is strictly dominated by n

in conclusion, to find DF(n),

DF(n)=\left(\{m:n\prec m\}\cup\bigcup_{\substack{n\text{ immediately }\\\text{ domates }m}}DF(m)\right)-\{m:n\text{ strictly doms }m\}

finally, we need to rename variables. we do by graph traversal.

Week 1. Jan 10

lexing/tokenization

Week 2. Jan 17

computing delta

interpreting REs by derivatives

parsing

Week 3. Jan 24

LL parsing

earley parser

LR parsing

Week 4. Jan 31

LR(0) parser

LR(1) parsing

LALR(1) parsing

AST

semantic analysis

Week 5. Feb 7

symbol table

AST traversal

types

Week 6. Feb 14

dataflow analysis

live variable analysis

simple liveness analysis

Week 8. Feb 28

reachable statement analysis

available copies analysis

dataflow analysis framework

iterative solving

Week 9. Mar 7

IR

translating from source language to IR

arrays

IR lowering

Week 10. Mar 14

canonicalizing cjumps

instruction selection

x86 ISA

tiling call/return

Week 11. Mar 21

register spilling

compiling OO features

method dispatch

interfaces

instanceof

Week 12. Mar 28

register allocation

x86 peculiarities

mov coalescing

compiling FP features

CPS transformation

Week 13. Apr 4

constant propagation (with cond branches)

abstract interpretation

static single assignment

conversion

`mov` coalescing