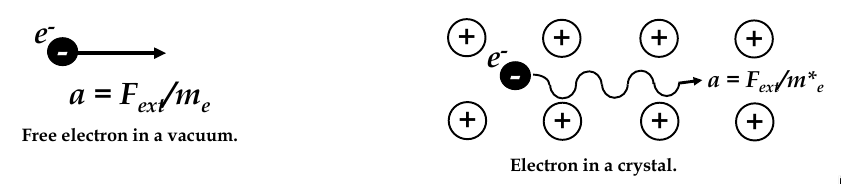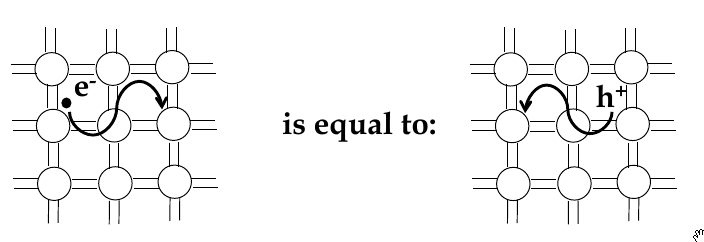ECE 209 Midterm Notes

Materials Structures

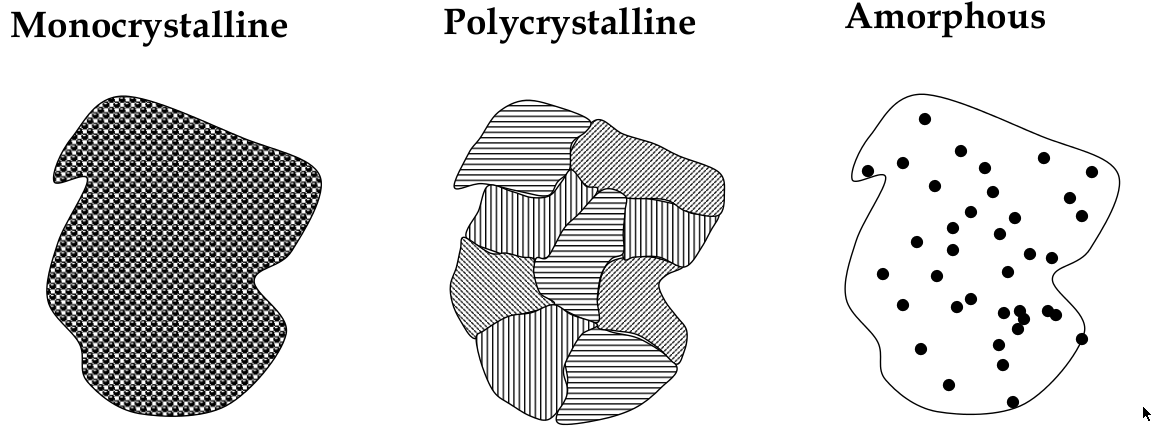
Crystalline, polycrystalline, and amorphous

• materials can be classified into the 3 types: crystalline, polycrystalline, and amorphous

Crystalline

• crystalline solid: a solid in which atoms bond in a regular pattern to form a periodic array of atoms
• long range order: happens in a crystalline solid b/c periodicity;
  • means that each atom is in the same position relative to its relative
  • perfect order yay

Polycrystalline

• long-range order exists over small distances only
• has small crystal “grains” that are randomly oriented

Amorphous

• no long-range order! It’s completely disordered

Crystals in microelectronics

• different types of crystals should be used for different things in microelectronics
• Polycrystalline silicon used for:
  • gate material in MOS transistors
  • interconnect lines
• Amorphous silicon used for:
  • switching transistors for AMLCD displays
  • solar cells
• crystalline used for all kinds of things
  • attractive because of perfect order, which:
    • simplifies theories
    • repeatable, predictable and uniform properties for material processing

Silicon structure; covalent bonding

• covalent bonding: shares atoms to make a full valence shell (8 atoms for Si)
  • Si ends up in a tetrahedral shape due to the repulsion interactions
• silicon has a diamond unit cell

Unit cell

• lattice: infinitely repeating array of geometric points in space
• lattice crystal structure: a lattice, with atoms on the lattice points
• unit cell: smallest repeating structure in the lattice crystal structure
  • lattice constant: the length of the cubic unit cell - a
  • interatomic distance: the distance between atoms in a unit cell (not the same as a!!)

Bragg’s Law

• to measure the lattice constant of an atom, use x-ray diffraction
• for a wave incident on a plane of atoms, reflective pattern will have bright and dark spots from constructive and destructive interference
• Bragg’s Law for where bright spots appear:
  $$ n\lambda = 2dsin\theta $$

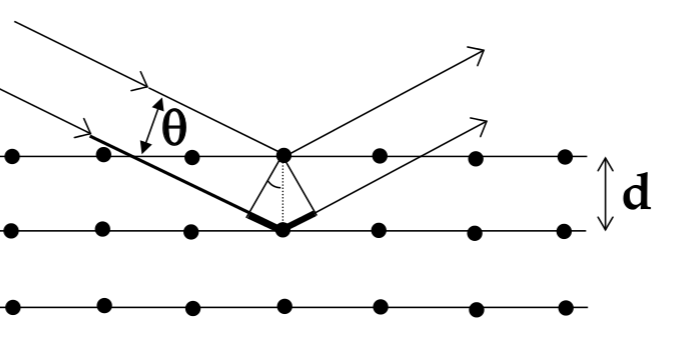
- crystal characteristics (and x-ray diffraction) depend on the direction you are looking

Miller indices

• since direction matters, we need a way of classifying it
• miller indices: sets of 3 numbers that are used to identify groups of crystal planes and directions

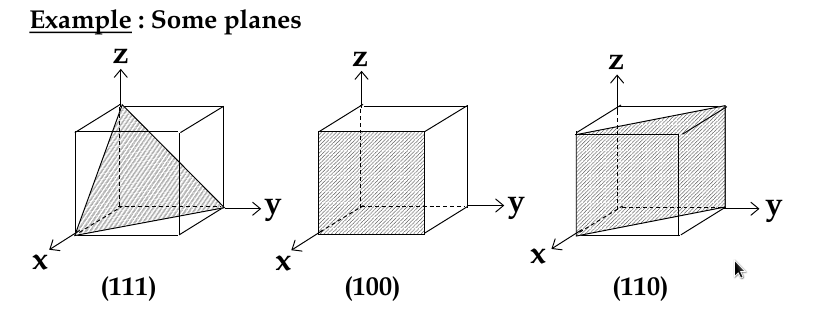
Miller Indices for Planes

• set up 3 axes along 3 adjacent edges of unit cell
• choose unit cell length as unit distance along respective axis (a = 1)
• chose a plane that passes through the centre of particular atoms. The plan intersects the axes at distances x1,y1, za (in example below, 1,2, 2/3)
• take reciprocals of interception co-ordinates, change to set of smallest ints, write as (hkl)

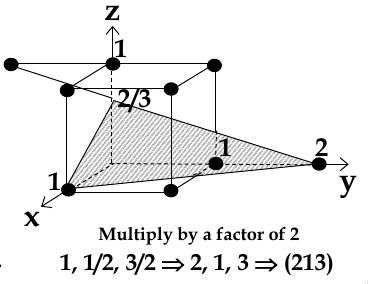
Miller Indices for Directions

• take a parallel line which passes through the origin
• not the length of the projections of this line on x,y,z axes
• change to smallest ints
• write as [hkl]

Family of Planes and Directions

• family of planes: {hkl)
• family of directions:
• represents all equivalent planes/directions
• {110} represents all planes (110), (011), (101), etc

Transmission Electron Microscopy

• TEM samples thinned and illuminated with accelerated electrons
• electrons are absorbed in the sample depending on thickness and material composition
• intensity variation of the transmitted electron beam is observed using a viewing screen

Scanning Tunneling Microscopy

• scans across the surface of sample with a very sharp needle
• needle kept 1nm from surface, voltage applied between needle and sample
• current used as feedback signal to determine gap size (can only give information about surface of sample)

Silicon bulk crystal growth

• to make ICs, we have to grow perfect crystals on a commercial scale
• for crystal growth, a saturated solution or a molten liquid is usually used.
• the material is then grown on a seed crystal which acts as a template for the new growth
• for silicon:
  • raw material: silicon dioxide
  • reduction => metallurgical grade polycrystalline Si
  • purification => electronic grade polycrystalline Si
  • melting & growth => crystalline bulk Si
• during melting and growth, a seed crystal is pulled slowly out of a bath of molten and rotated slowly
  • this is Czochralski (Cz) crystal pulling
• after growth, ingot is trimmed and sliced into wafers

Epitaxial growth

• electrical properties of Si are controlled roughly when the basic wafers are produced, but more precise cotrol is needed for reliable devices
• the top few microns of the wafer are where devices are made
  • this region must be well controlled
• achieved by growing a even more perfect crystal layer on top of the wafer
  • called the epitaxial layer
• during epitaxial growth, the surface of the wafer acts as the template
• decomposes Si-containing gases in chemical vapor dposition
• monolayer : a layer one atom thick

Molecular beam epitaxy

• a technique for growing thin layers
• a steam of neutral atoms or molecules are evaporated from a heated cell
• then incorporated into the growing film onto a heated target
• is $$$ $ b/c:
  • only one wafer can be used at a time
  • wafer must be small to get uniform layer
  • very good vacuum required

Epitaxy principles

• major feature of epitaxy is that the newly deposited film precisely follows the crystalline form of the substrate template
• adsorption: proces of atoms attaching themselves to the surface
• adsorption can occur anywhere on the surface with equal probability, so layer is unlikely to be crystalline
• for crystalline growth, absorbed atoms must be able to find the minimum energy positions
  • the ad-atoms must be able to move along the surface
• heat up the substrate during epitaxy to allow movement
  • if not hot enough, the ad-atoms stick where they land and the film is amorphous

Modifying Crystals

• to make an electronic device, crystals need to be modified and shaped according to the needs of the device
• examples: introducing impurities, etching/shaping

Ion implantation

• ionized impurities are accelerated into an electric field and “smashed into” Si surface
• depth of penetration determined by:
  • accelerating voltage
  • masses of ions and target atoms
  • crystal direction (density of atoms)

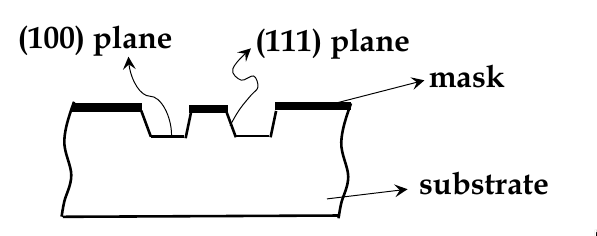
Etching and micromachining

• sometimes you need to etch crystals to get certain structures
  e.g. for making DRAMs, you need to etch deep tranches to make trench-capacitors
• wet-etching: uses liquid chemicals to remove materials from a wafer
• isotropic etching: chemicals etch at the same rate in all directions
• anisotropic etching: chemicals selectively etch one crystal plane more
  • see example below. KOH etches (100) faster than (111) planes

Atomic Structure

Nature of light

• classic physics: light is an electromagnetic wave w/ perpendicular field Bx and Ey
• electric field is given by the following equation:
  $$ E_y = E_o sin(kx - \omega t) $$
• where:
  • k = 2π/λ - the wavenumber (λ is the wavelength of light)
  • ω = 2πf - the angular frequency (f is the freq of light)
  • c= ω/k = fλ - speed of light / wave velocity
• light intensity is given by:
  $$ I = \frac{1}{2} c \epsilon_o E_o^2 $$

Experimental Evidence of Light as EM Wave

• interference and diffraction
• Young’s double-slit experiment
  • expand

Photo-emission (photoelectric effect)

• when a metal electrode is illuminated with light, it emits electron (can create a current with this!)
• light must possess the energy needed to “free” the electron from the metal (W)
  • any excess energy it possesses will become the kinetic energy of the electron
• according to classical theory of light, the energy balance should be: E _L = W + E _K
  • if we reduce E _L by reducing the intensity of the light, E _K should also decrease
• if light intensity is increased -> saturation current increases
  • more electrons emiited
  • same voltage is required to stop the current, thus the kinetic energy of the electrons is the same
• classical theory of light can’t explain this!

Photons

• light contains particle of fixed energy called photons
• light frequency increases -> energy of light increases
• E _L = hf
  • h = Planck’s constant

Wave-Particle Duality

• light has properties of both a wave and a particle
• light waves consist of a stream of photon particles, each with energy hf
  • energy carried by the wave consists of discrete lumps or quanta

De Broglie relationship

• electrons also have a wave-particle duality
• particle-like properties confirm with cathode ray tube (1897)
• deBroglie predicted that electrons would have a wavelength:
  $$ \lambda = \frac{h}{p} $$
  • where p = mv is the electron momentum
• confirmed with electron diffraction experiment

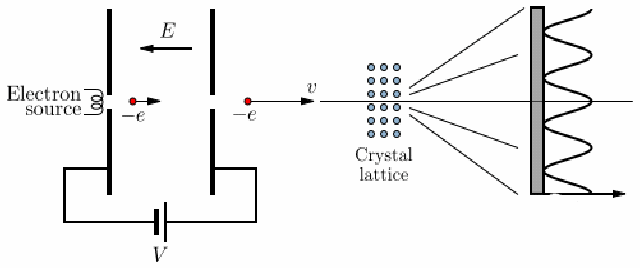
Electron Diffraction Experiment

• voltage accelerates electron, strikes a thin carbon layer, hits the screen
  • produce a glow of light proportional to their number and energy
    
• using this, get the deBroglie relationship

Wavefunction, wave vector, and Schrödinger equation

• for an electromagnetic wave:
  $$ E_y (x,t) = E_o sin(kx - \omega t) $$
• for an electron wave:
  $$ \psi = A sin(kx - \omega t) $$
  $$ \psi = Ae^{j(kx - \omega t)} $$
• where:
  • k = 2π/λ - the wave vector
  • ω = 2πf
  • A = constant
• can separate the time-dependent and space-dependent parts and write:
  $$ \psi = Ae^{jkx}e^{-j\omega t}$$
• wave function related to the probability of finding the electron at a given point in space and time
  • represents the distribution of the electron wave in time
• Probability = ΨΨ* = |Ψ| ²
  • probability is a real value

Wave Vector and Potential Energy

• electron wave momentum is related to the wavelength by this equation: p = h/v
• momentum is a vector - therefore we need a vector form of the wavelength
• wave vector:
  • direction: direction of wave travel
  • magnitude: k = 2π\λ
• momentum now written as:
  $$ p = \frac{h}{2π}k$$
• kinetic energy is:
  $$ E_k = \frac{p^2}{2m} = \frac{h^2}{8π^2}\frac{k^2}{m}$$
• electron also has electrostatic potential energy
  • defined as the work done in pulling the negatively chargely electron from an infinite distance to a distance, r, from the positively charged nucleus:
    $$ E_p = \frac{-e^2}{4πε_0 r} $$
    -total energy is E = E _k + E _p
    $$ k = \frac{2π}{h} \sqrt{2m(E - E_p)} $$

Schrodinger’s Equation

• describes the electron wave function
• if you know the electron potential energy and boundary conditions, you can calculate the parameters of electron orbital (wave function and energy)
  $$ \frac{d^2 \Psi}{dx^2} + \frac{8\pi^2 m}{h^2}(E - E_p )\Psi = 0 $$

“Electron in a box” problem

Electron in a 1D Potential Well

-setup:
- inside the box, potential energy is zero
- outside, is infinitely large
- we need to find the wave equation

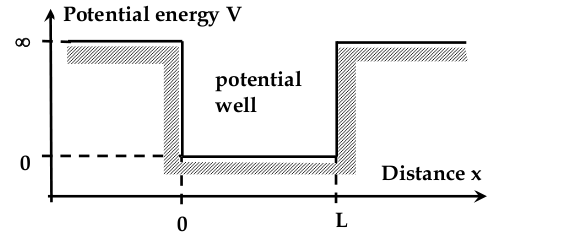
$$ \frac{d^2 \Psi}{dx^2} + \frac{8\pi^2 m}{h^2}(E - V)\Psi = 0 $$

• assumptions:

  • the case is time-independent
  • wave function is continuous, smooth, and single-

• Boundary conditions:

  1. For x<0 and x>L, the term Vψ dominates
     $$ -V\Psi = 0 \\ \Psi = 0 |\Psi|^2 = 0 $$
     electron cannot be outside the well
  2. Since d ² ψ/dx ² must be continuous, ψ = 0 at x={0,L}

• Differential equation:

  • second order differential equation to solve for within the well
  • general solution equation is:
    $$ \Psi (x) = 2Ajsin(\frac{n\pi x}{L}) $$
  • can solve for A because we know the probability of electron being in the box is 1 (integral of equation from 0 to L is 1)
  • final form of the equation is:
    $$ \Psi (x) = j(\frac{2}{L})^{\frac{1}{2}}sin(\frac{n\pi x}{L}) $$

Electron Energy in Potential Well

$$ E = \frac{h^2 n^2}{8mL^2} $$
- energies E(n) are the eigenenergies of the electron
- energy is quantized
- n is the quantum number
- min energy is at n=1, this is the ground state
- energy of electron wave can only have discrete values
- energy of electron particle can take any value

Uncertainty Principle

• free electron:
  • has single energy, momentum, wavelength - Δp = 0 (uncertainty 0)
  • electron wave is spread all over the space, so Δx = ∞
• electron in a potential well:
  • Δx = L
  • Δp = hk/π
    • for n=1, k: = π, Δp = h/L
      $$ \Delta x \Delta p = L \frac{h}{L} = h $$
• Heinsenberg’s uncertainty principle: we cannot simultaneously and exactly know both the position and momentum of an electron along a given co-ordinate

Tunnelling

• important application of the uncertainty principle
• if an electron of energy E meets a potential energy barrier of height V_o_ > E, it might leak (“tunnel”) throug the barrier
  • probability of that depends on the energy and width of the barrier

Hydrogen atom

• consider the H atom: an electron attached to a nucleus
  • electron is electrostatically bound to a single proton
  • since proton is so big, it behaves more like a particle
• potential energy:
  $$ V(r) = \frac{-Ze^2}{4\pi \epsilon_o r} $$
• where:
  • Z = number of electrons
  • r = (x ² + y ² 2 + z ² ) ^1/2
• considerng electron in H atom as confined in a potential well with PE V(r), electron’s wave function can be derived to be:
  $$ E = \frac{-Z^2 e^4 m}{8h^2 \epsilon_o^2}\frac{1}{n^2} $$
  • different energy values (different values on) are called Energy Levels

Atomic Spectra

• electrons can be excited into higher energy levels - requires energy
• they can also return to a lower levels - releases energy in the form of a photon with appropriate energy E = hf = E _higher - E _lower

Quantum Numbers

Principal Quantum Number, n

• determines the radius of electron orbit and the energy level

Orbital Angular Quantum Number, l

• determines the shape of the orbital
• the electron wave at each orbit (at each r) may be standing or moving along the orbit
• wave must be continuous and smoothly varying
  • must fit an integral number of wavelengths: lλ = 2πr
    $$ L = pr = \ell \frac{h}{2\pi} $$
• L is the angular momentum, which is quantized.
• l can take any value from 0 to (n-1)

Magnetic Quantum Number, m _l

• determines orientation of the orbital in space (the tilt of the electron cloud), and the energy of its electron in a magnetic field
• angular momentum about the electron orbit is quantized as:
  $$ L_z = \frac{m_\ell h}{2\pi} $$
• -l ≤ m _l ≤ l

Electron Spin Quantum Number, m _s

• determines the rotation of electron about its own axis
• has the values 1/2, -1/2 (spin up, spin down)

The Full Sert of Quantum Numbers and Values

n = 1, 2, 3, … z
l = 0, 1, 2, 3, … (z-1)
m _l = 0, ±1, ±2, ±3, … ±(z-1)
m _s = ±1/2

Summary of Quantum Numbers

• Radius of orbit → n
• Orbital angular momentum → l
• Tilt of orbit’s plane → m _l
• Spin of electron → m _s

Electron Clouds

• we can define electron clouds corresponding to different combos of quantum numbers
  • probability density distribution

Multi-electron atoms, Pauli principle, and the periodic table

• building atoms requires an organization of Z electrons around the nucleus
• two principles for doing so:
  • electrons will occupy the lowest possible available energy state
  • no more than one electron can have the same set of quantum numbers (Pauli’s Exclusion Principle)

• start filling the atomic states (quantum number states) with electrons

  • e.g.: For Lithium, there are 3 electrons:
    • n = 1, l = 0, m _l = 0, m _s = 1/2
    • n = 1, l = 0, m _l = 0, m _s = -1/2
    • n = 2, l = 0, m _l = 0, m _s = 1/2

• notation:
  
  

Band Structure

Hydrogen molecule and molecular bonding

• when atoms interact, they change behaviour
  • no two electrons in an interacting systems may occupy same quantum state
• consider the case of two H atoms
  • when they are infinitely far apart, they have the same wave function
  • when they approach each other, their wave functions overlap and two new molecular wave functions emerge (see the image below for the two new functions
• molecular wave functions are linear combinations of atomic orbitals; in this case, one is the sum and one is the difference
• Ψ _σ is more confined to the nuclei, whereas Ψ _σ* is more spread
  • thus, Ψ _σ* has higher energy
  • Ψ _σ then is more energetically favourable, so both electrons occupy this state
• bonding orbital: the wave function Ψ _σ corresponding to the lowest energy level
• antibonding orbital: Ψ _σ*
• total energy of two electrons in H ₂ molecule is lower than in two single H atoms
  • one electron has to flip its electron spin but the energy gain due to dropping to bonding orbital is higher than the energy spent

Energy band formation; metals, semiconductors and insulators

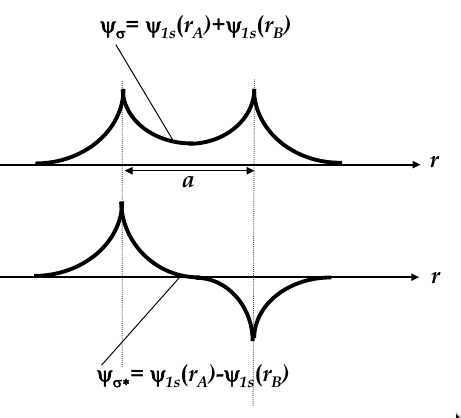
• consider 3 hydrogen atoms. They will also add their atomic wave functions, like so:
  
• the more atoms in our function, the more molecular orbitals they’ll form. n atoms = n orbitals
• if an energy band is not entirely filled, there are states available for electrons. Consider N Li atoms (2s half filled)
  • thermal energy is enough at room temp for electrons to jump between nearest energy levels
  • since the levels may belong to different atoms, electrons can easily travel from atom to atom conducting current

Hybridization

• 2s and 2p energy levels are close, so when they approach each other, 2 2s and 2 2p orbitals can mix to form hybrid orbitals
  • hybrid orbitals directed in tetrahedral directions and have the same energy
• process called sp ³ hybridization

Energy Bands

• when interatomic distance decreases so that electrons interact, their energy levels broadens (splits) into bands
• there are 2N states in the 2s-band, 6N states in 2p-band
• in diamond crystal, bonding and anti-bonding orbitals split and form valence band and conduction band , respectively
• band gap - E _G - the difference in energy between the conduction and valence bands

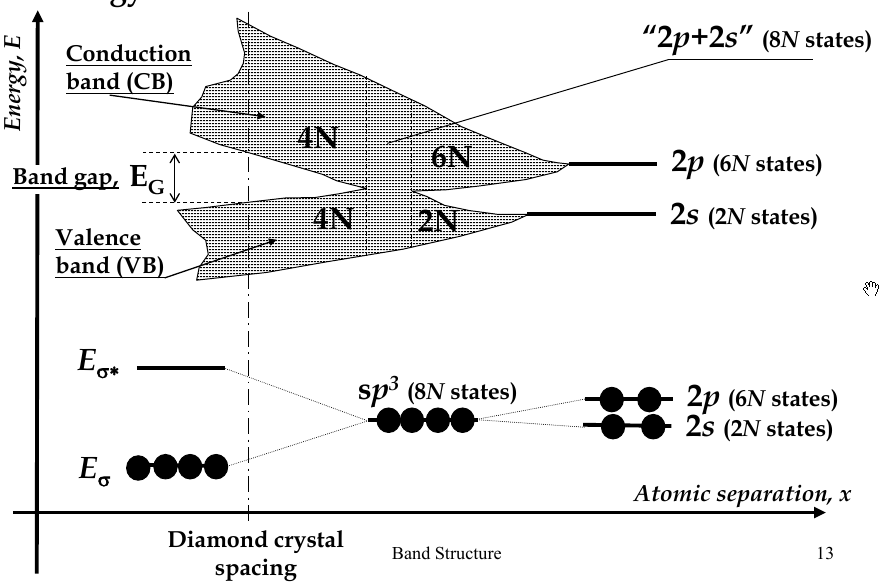
Fermi Energy

• at T=0K, all electrons will occupy states with lowest energy (valence band), so conduction band empty
• fermi energy (E _F ) = energy level corresponding to highest filled electron state at 0K.
• as T increases, bands above E _F start to get filled
• to conduct electric current, there must be vacant states in the band
• no states available in energy levels within each band, no conduction

need more but confusing tho

Effective mass

• acceleration of an free electron in vacuum is a = F _ext / m _e , m _e = electron mass in vacuum
• in a solid, electron interacts with crystal lattice atoms and experiences internal forces F _int
• thus, acceleration is: a = (F _ext + F _int ) / m _e

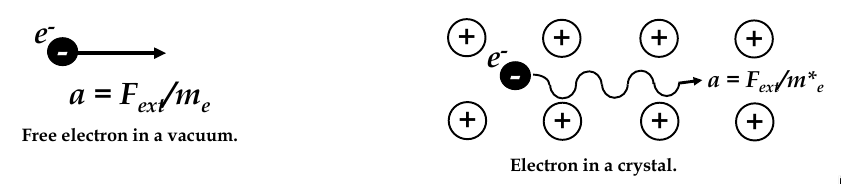
• since atoms in a crystalline solid are periodically positioned, variation of F _int is also periodic, we can simplify our acceleration equation:
  $$ a_crystal = \frac{F_ext}{m_e^*}
• where m _e ² is the effective mass of the electron
• effective mass depends on the material

Electrons and holes

• in semi-conductors, in order to get excited to empty states, electrons jump across the band gap
• when excited to the conduction band, a vacant state is left in the valence band
  • this is called a hole - the absence of an electron
• electrical conduction in a semiconductor involves movement of electrons in the conduction band and holes in valence band
  • electron and hole currents

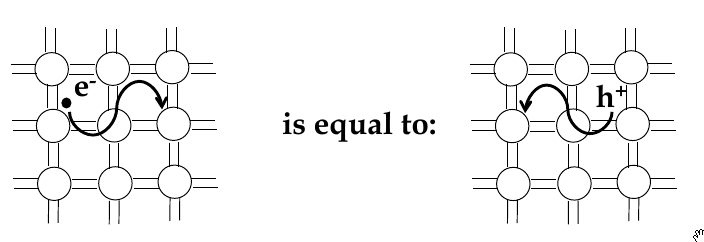
Intrinsic Semiconductor

• a pure semiconductor (no foreign atoms present) is an intrinsic semiconductor
• electrons and holes can only be created in pairs (electron-hole pairs)

Carrier Generation

• electron-hole pair generation: the act of exciting an electron from the valence band to the conduction band
• electrons can be excited even though E _T is much smaller than E _G because atoms in the crystal are constantly vibrating (due to thermal energy) and deforming interatomic bonds
  • thus, some bonds may be overstretched, and the bond energy can be smaller than thermal energy
• electron concentration in the conduction band, n, (electrons per cm ³ ) is always equal to hole concentration in the valence band, p, (holes per cm ³ )
  • n = p = n _i
  • n _i = intrinsic carrier concentration
• g _i : rate of generation

Recombination

• opposite of carrier generation: the act of an electron falling back to VB
• excess energy is released in the form of heat or light
• rate of recombination, r _i , is proportional to equilibrium concentration of electrons/holes
• r _i = αn ₀ p ₀ = αn _i ²
  • α = constant
  • n ₀ = equilibrium electron concentration
  • p ₀ = equilibrium hole concentration
• in steady state, r _i = g _i

Conduction

• takes place only when electron-hole pairs are created
• conduction not great in intrinsic semiconductors at room temperature

Doping, extrinsic semiconductors

• doping: creation of carriers in semiconductors by introducing impurities
  • we get extra carriers, and better conductivity
• doped semiconductor = extrinsic semiconductor
• n-type semiconductor: predominant electron concentration
• p-type semiconductor: predominant hole concentration

n-type doping

• n-type Si obtained by adding small amounts of group V elements (P, As, Sb)
  • these elements have 5 valence electrons, but the atoms bond to Si (4 e ^- ), so one of the electrons is weakly bonded to the impurity atom
  • very tiny amount of energy needed to excite electrons, so at most temperatures most of the donor electrons will be ionized

p-type doping

• p-type Si obtained by adding small amount of group III elements (B, Al, Ga, In)
  • these elements have 3 valence electrons, atoms bond to Si (4 e ^- ), one of the bonds will miss an electron
• impurity atoms = acceptors (accept an extra electron)

Carrier concentration

• how to calculate the number of electrons and holes available for conduction? need to know:
  • number of states available at a particular energy to be occupied
  • fraction of these states that are in fact occupied at a particular temperature
    $$ n_o = \int_{E_c}^\infty \! f(E)N(E) \, \mathrm{d}E. $$
• where:
  • N(E) - density of states
  • f(E) - Fermi function

Density of States

• DOS: number of available states per unit volume
• expressions for valence and conduction band are:
  $$ N_V(E) = \frac{8\sqrt{2}\pi}{h^3}(m_p^*)^{\frac{3}{2}}(E_V - E)^{\frac{1}{2}} for E < E_V \\ N_V(E) = \frac{8\sqrt{2}\pi}{h^3}(m_n^*)^{\frac{3}{2}}(E - E_C)^{\frac{1}{2}} for E > E_C $$

Fermi function

$$ f(E) = \frac{1}{1 + e^{\frac{E - E_F}{kT}}} $$
- Fermi-Dirac distribution function gives us the probability that an available energy state at E will be occupied by an electron at temperature T
- probability that an available energy state will be occupied by a hole is 1 - f(E)
- at E=E _F , f(E) = 1/2
- E _F in intrinsic material: middle of band gap b/c concentration of holes in VB = concentration of electrons in CB
- E _F in n-type material: closer to E _C because the concentration of electrons in CB is higher than concentration of holes in VB
- E _F in p-type material: close to E _V because concentration of holes in VB is higher than concentration of electrons in CB

Equilibrium Carrier Concentration

• for equilibrium conditions, can use the effective density of states * N _C at energy E_C. Thus:
  $$ n_0 = N_C f(E_C) $$
• Then, f(E _C ) can be expressed as:
  $$ f(E_C) = \frac{1}{1 + e^{\frac{E_C - E_F}{kT}}} = e^{-\frac{E_C - E_F}{kT}} $$
  $$n_0 = N_C e^{-\frac{E_C - E_F}{kT}} $$
  • where N _C is a constant
• similarly, concentration of holes is:
  $$ p_0 = N_V [ 1 - f(E_V) ] $$
• where N _V is the effective density of states in the valence band
• $$ p_0 = N_V e^{-\frac{E_F - E_V}{kT}} $$
  • where N _V is a constant

Mass Action Law

$$ n_0 p_0 = n_i^2 \\ n_0 = n_i e^{\frac{E_F - E_i}{kT}} \\ p_0 = n_i e^{\frac{E_i - E_F}{kT}} $$

Conductivity and mobility

• current of electrons and holes depends on:
  • carrier concentration (n, p)
  • carrier speed (v _n , v _p )
  • carrier charge (q or e)
• current density can be written as:
  $$ J_n = nev_n \\ J_p = pqv_p $$
• at low electric field, the carrier velocity is proportional to the field: υ = με
• the proportionality constant μ is called the mobility
• total current density is: J = σε
  • ε is called the conductivity

Hall Effect

• mobility in semiconductors can be estimated using the Hall effect
• if we apply electric field E _x in direction x across a semiconductor and submit it to magnetic field B _z in direction z, then another electric field E _y (Hall field) occurs perpendicular to both E _x and B _z
• E _y occurs due to deflection of electrons from direction z due to Lorentz force
  F _y = -ev _x B
• electron velocity in x-direction: v _x = μ _x E _x
• in steady state, deflection is steady and Hall field counterbalances Lorentz force:
  • eE _H = ev _x B _z
  • eE _H = J _x B _z /n
  • E _H /J _x B _z = 1/en = R _H - Hall coefficient
• μ = | σR _H | - Hall mobility

Haynes-Shockley Experiment

• direct way of measuring mobility

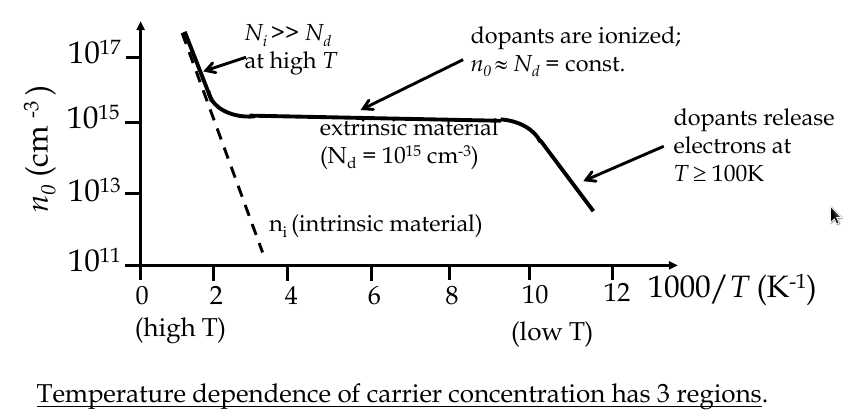
Temperature dependence of carrier concentration

$$ n_i (T) = 2{\frac{2\pi kT}{h^2}}^{\frac{3}{2}}{m_n^* m_p^*}^{\frac{3}{4}}e^{\frac{-E_G}{2kT}} $$

Compensation doping

• semiconductor could have both acceptors and donors in it: this is compensation doping
• the concentrations of electrons, holes, donors and acceptors can be obtained from space charge neutrality law
  • the material must remain electrical neutral overall
• p ₀ + N _d ⁺ = n ₀ + N _a ^-
• a material doped equally with donors and acceptors becomes “intrinsic” again

Diffusion Current

• diffusion: net motion of carriers from regions of high carrier concentration to low carrier concentration if there is non-uniformity (gradient) of carrier concentration

need more

Direction and indirect bandgap semiconductors

• dielectrics and semi-conductors behave essentially the same way - the only difference is the bandgap width
• photons with energy exceeding E _g are absorbed by giving their energy to electron-hole pairs
  • may or may not reemit the light during recombination depending on whether the gap is direct or indirect
• direct bandgap semiconductors: electron drops from bottom of CB to top of VB, excess energy emitted as a photon
  • also known as radiative recombination
• indirect bandgap semiconductors: recombination occurs in two stages via recombination centres (usually defects) in the bandgap:
  • electron falls from bottom of CB to the defect level, then down to the top of VB
  • electron energy is therefore lost in two portions by the emission of phonons (lattice vibrations)
  • this process is also known as non-radiative recombination

Photoconductivity

• increase of conductivity under illumination
  $$ \Delta \sigma = \sigma_photo - \sigma_dark = \frac{e\eta I\lamda \tau (\mu_e + \mu_h)}{hcD}
• η is quantum efficiency, and τ is average excess carrier lifetime

Energy-band diagrams and MOSFET