As stated in my last post, I’ve been working on a toy compiler. One thing that good type-checkers in compilers do is give you helpful suggestions when it fails to type-check. In this post I want to talk about the type-checker suggesting spelling corrections for you. The following is an example of the OCaml REPL suggesting a spelling correction for you.
# let foo x = x + 1;;
val foo : int -> int = <fun>
# boo (2 + 1);;
Error: Unbound value boo
Hint: Did you mean foo?Let’s take a look at how the compiler implements this!
You’ll find the spellcheck function in
utils/misc.ml
[link].
The function spellcheck in turn uses the
edit_distance
[link]
function.
The edit_distance function is the standard dynamic programming solution to
computing edit distances.
If you are anything like me, you wouldn’t write dynamic programming code unless it was absolutely critical. I find dynamic programming to be aesthetically unpleasant, and you’d need to pay me to write code like that. There’s also no good way do early cut-off without making the code even more complicated. Is there a way around dynamic programming? Fortunately yes!
Levenshtein Automata
With some quick Googling of “Levenshtein edit distance” and following links in
Wikipedia you’ll run into the Wikipedia page for Levenshtein
Automaton.
“A Levenshtein automaton for a string w and a number n is a finite state
automaton that can recognize the set of all strings whose Levenshtein distance
from w is at most n.”
As we will see below, thankfully, constructing the Levenshtein automaton does
not involve dynamic programming.
This is almost what we want, if take a look at the spellcheck function, you’ll
see that it suggests strings with the best edit distance, so we not only want to
know that the edit distance is less than some k, but want to also rank the
strings by their edit distance.
Below I will discussing recovering edit distances from Levenshtein automaton. But first a tangent and a bit of a rant!
A Tangent: Thoughts on Automata from a PL Perspective
I find it a little odd that when studying Automata Theory, finite state
automata/machines (FSA/FSM) are almost always treated as accept/reject gadgets
(see below for thoughts on finite state transducers).
The accept/reject versions do have a richer theory in some sense.
You have more operations available to you for composing them.
Operations such as concatenation and Kleene star make more sense in this
setting.
But from a PL perspective, it is very limiting to be only working with gadgets
that map strings to the set {accept, reject}.
Automata Theory also studies finite state transducers (FST) which map strings in an
input alphabet to strings in the output alphabet.
But using FSTs as maps from strings to single character strings in the output
alphabet gets hairy really quickly.
You start to require sentinel end of input characters or more non-determinism.
For these use cases, it is much nicer to think of FSM as maps from input strings
to their final states.
For operations, you still have access to the union and intersection operations,
but the programmer has decide what the final states mean after these operations
— the theory doesn’t automatically dictate this to be {accept, reject}.
It also feels odd to compute which state the FSA ends up in, and then throw away that information. For Levenshtein Automata, it turns out that states of Levenshtein Automata carry the edit distance of strings, throwing this away feels stupid!
Recovering Edit Distances from Levenshtein Automaton
Below is a diagram of the non-deterministic Levenshtein Automaton for the word “SALAD” from the paper by Touzet [1]. The paper uses to indicate the maximum edit distance that will be matched by the automaton, and in the diagram below .
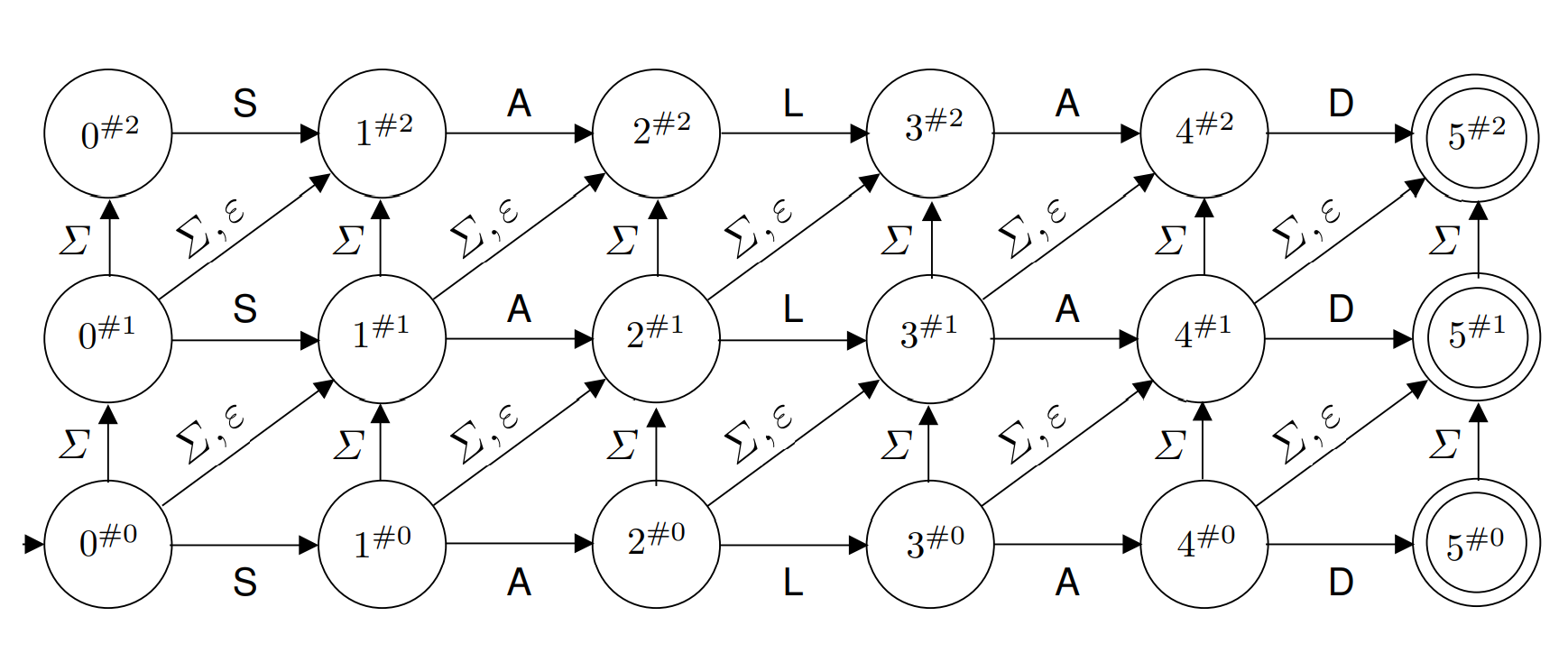
In the diagram above the notation stands for “ characters have been read in the pattern and errors have been recorded” [1]. “Horizontal transitions represent identities, vertical transitions represent insertions, and the two types of diagonal transitions represent substitutions () and deletions (), respectively” [1].
It should immediately jump out to us that since the states of the automaton are labeled with error counts the final states are therefore labeled with edit distances! If we enter multiple final states, the minimal error count will be the edit distance. So if we were using the Levenshtein Automaton for filtering words, we can use the labels to rank strings by their edit distance!
Using Levenshtein Automata, we can get away from dynamic programming. But even this has it’s problems!
Problems Levenshtein Automaton
First, a matter of aesthetics! I wanted to get get away form dynamic programming because I find it aesthetically unpleasant, but I find computing -closures to be just as unpleasant. -closures also make it difficult to predict behaviour at runtime, but this can be avoided by converting the non-deterministic finite-state automaton (NFA) into a deterministic finite state automaton (DFA).
I haven’t read the paper by Schulz and Mihov [2], but from the diagrams and a quick cursory read through some of the definitions it seems some of this can be mitigated with their subsumption triangles. In fact, one of their results (Theorem 1) is that you can create a Deterministic Levenshtein Automaton for a word which has size linear in
But still… The size of the automaton being dependent on the word is a little annoying. As stated above, we may want to compute the DFA from the NFA, and if we do this for large words, we’ll have to store a large DFA in memory.
This is where Universal Levenshtein Automaton come in!
Universal Levenshtein Automaton
Touzet [1] describes Universal Levenshtein Automaton in a fairly accessible
way, although some of the ideas presented are derived from the work of Schulz
and Mihov [2].
I recently followed the Touzet paper and implemented Universal Levenshtein
Automata in my library mula
(https://github.com/ifazk/mula/).
The paper is a really nice read, but I’ll explain some of the implementation
details in mula below.
Suppose we fix a string of length , and a maximal edit distance . Conceptually, we will be working with an encoding , where is a sentinel character. We will be comparing against a word , and we assume that has size . Again we will be conceptually be working with an encoding , i.e. has size .
Bit vectors
The first piece of machinery we will need are characteristic bit vectors. For a character and a string of length , the characteristic bit vector is a bit vector of length such that the -th character of the bit vector is if and otherwise. For example, , , , and .
For an index (the paper uses 1-indexing), we will have to compute . In my implementation I split this up into two cases, first where , and a second where .
For , this is just , it’s a character from .
- We can compute the number in the prefix of as .
- The overlap between and is for and .
- We can compute the number in the suffix of as .
- So .
For , we can follow similar steps to get .
Note: There is a typo in the Touzet paper in Definition 2. The paper asks us to compute , but this is undefined when .
Non-deterministic Universal Levenshtein Automata
Below is a diagram of the non-deterministic Universal Levenshtein Automaton for (shamelessly stolen from Touzet [1] again). It transitions on the bit vectors from the above.
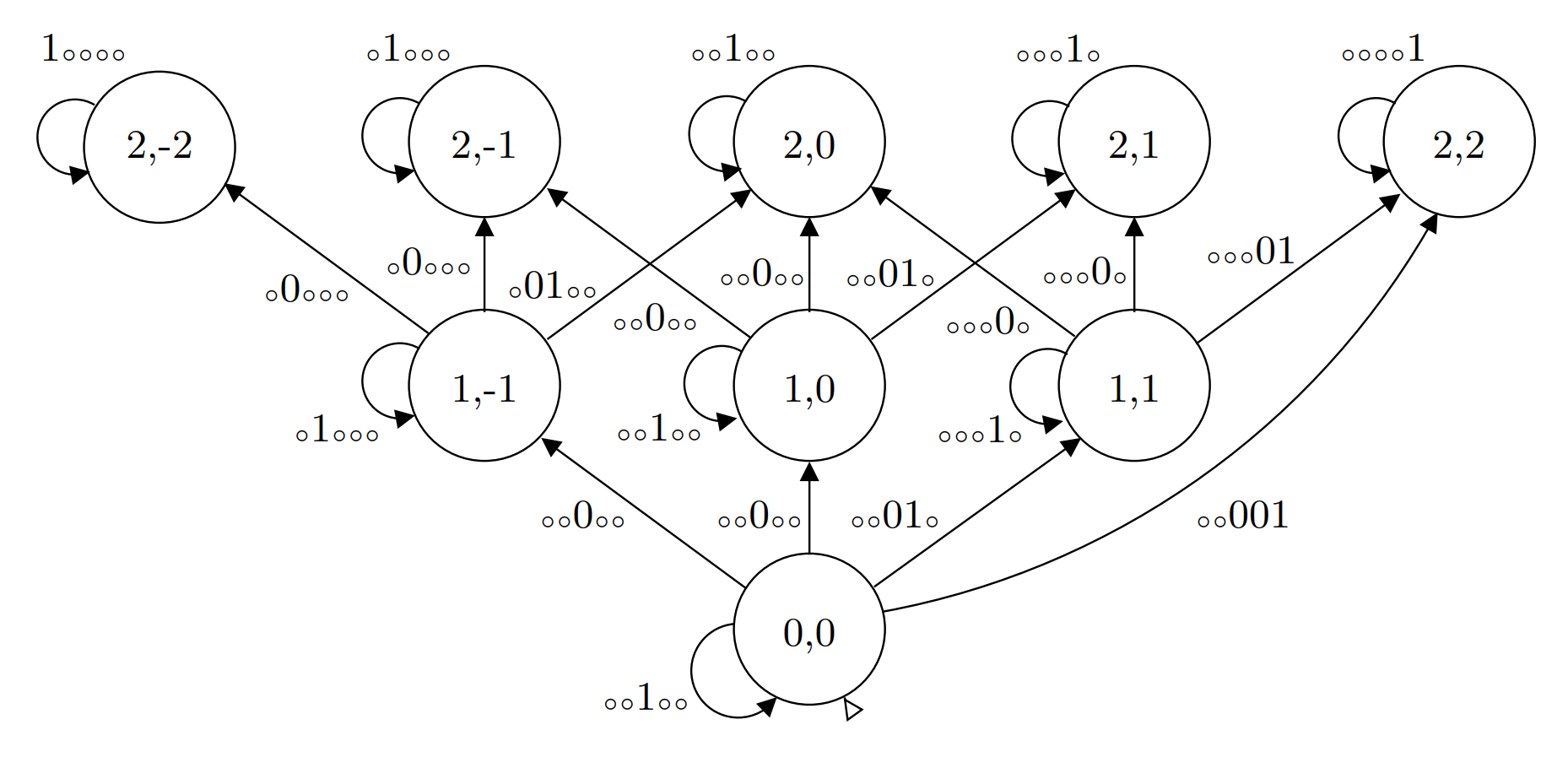
Transitions to the left are delete edits, transitions to the right are insert edits, and transitions upward are substitution edits. Supposed characters have been fed into the automaton. The labels should be read as “ errors have been recorded, and to keep the same number of errors, the -th of character must be the same as the -th character of ”.
The paper details a subsumption relation, so any state subsumes states
in the triangle above it.
For example, in the diagram above subsumes , , and
.
This means that after transitioning from a set of states to another set of
states, we can prune any subsumed states.
After pruning, there is a bound on how many states can be active in the
automaton, and it is .
The pruning is implemented in mula.
The Nice Parts of Universal Levenshtein Automata
Firstly, it gets rid of my last aesthetic complaint. We no longer have -transitions!
Secondly, the automata are independent of input strings, they only depend on .
Thirdly, the NFA is easily computable. Given an input state and a bit vector, we can easily compute its transition. If we are in lane , and the -th element of the bit vector is , then we stay in the same state. Otherwise, we make insert and substitution and delete transitions if possible. For insert and substitution transitions, the current error count must less than . For delete transitions, we look for the first bit in the bit vector to the right of the lane that is , and transition to that delete state. If all the bits to the right are , there will not be a delete transition. Here, right of the lane means the bits starting at the -th bit of the bit vector.
Fourthly, the bound on states being is really nice. Without the subsumption relation, the number of states at any given time could be quadratic in , but in Universal Levenshtein Automata it is linear in .
Lastly, we still have the nice property that states carry error counts.
What’s Missing from mula?
I only implemented matching with NFAs in mula.
It should be possible to pre-compute the DFA’s for up to and ship them
with the library.
It should also be possible to add other types of Levenshtein Automata to mula.
For instance, in optical character recognition, it is useful to count splitting
a character into two and merging two characters into one as single edits.
I currently have matching with the NFA, but there are use cases (e.g. suggestions in IDEs) where knowing exactly what has been matched is useful. I would like to additionally provide Finite State Transducers which output if we transition to the same state, and s when we transition to states with higher errors.
Conclusion
Universal Levenshtein Automata are really nice, and simple to implement! They allow you to avoid annoying programming like dynamic programming and computing -closures. If you don’t care about actual full edit distances, and only care about distances up to a limit, Universal Levenshtein Automata are probably what you want!
References
- Hélène Touzet. On the Levenshtein Automaton and the Size of the Neighborhood of a Word. LATA2016 - 10th International Conference on Language and Automata Theory and Applications, Mar 2016, Prague, Czech Republic. pp.207-218, 10.1007/978-3-319-30000-9_16.
- Klaus U. Schulz and Stoyan Mihov. Fast string correction with Levenshtein automata. IJDAR - International Journal on Document Analysis and Recognition volume 5, pages 67–85 (2002). 10.1007/s10032-002-0082-8
Further Readings
Levenshtein Automata in Python: A blog post about implementing Levenshtein Automata in python.
Lucene FuzzyQuery: This is a blog post about how this was implemented in Lucene. Using Python to generate a Java file really feels like a crime!
Levenshtein Automata in spelll:
This is an implementation of Levenshtein Automata in OCaml. It follows a
different implementation in
Python.
Proofs about Universal Levenshtein Automata:
This thesis proves some properties of Universal Levenshtein Automata.
I have not read the thesis, but did use Figure 9 to implement
Demarau-Levenshtein Automata (restricted edits) in mula.